Last Updated:
Written by:
Time to read:
Table of Contents – Class 11 Maths Chapter 2 Exercise 2.2 Solutions
Solved Examples before Exercise 2.2
Example 7. Let A = {1, 2, 3, 4, 5, 6}. Define a relation R from A to A by
R = {(x, y) : y = x + 1 }
(i) Depict this relation using an arrow diagram.
(ii) Write down the domain, codomain and range of R.
Answer 7.
(i) R = {(1,2), (2,3), (3,4), (4,5), (5,6)}
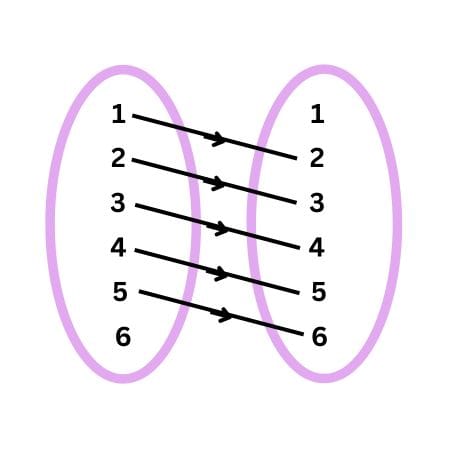
(ii) Domain ={1, 2, 3, 4, 5}
Range = {2, 3, 4, 5, 6}
Codomain = {1, 2, 3, 4, 5, 6}
Example 8. The Fig 2.6 shows a relation between the sets P and Q. Write this relation (i) in set-builder form, (ii) in roster form. What is its domain and range?
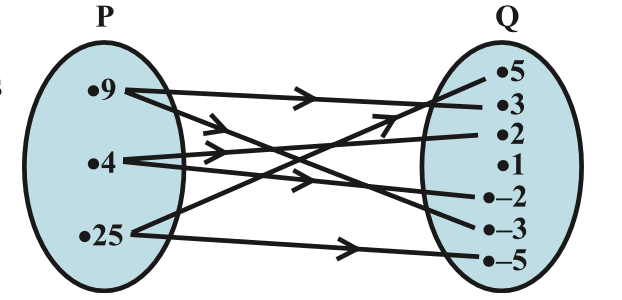
Answer 8. (i) In set-builder form, R = {(x, y): x is the square of y, x ∈ P, y ∈ Q}
(ii) In roster form, R = {(9, 3), (9, –3), (4, 2), (4, –2), (25, 5), (25, –5)}
The domain of this relation is {4, 9, 25}.
The range of this relation is {– 2, 2, –3, 3, –5, 5}.
Note that the element 1 is not related to any element in set P.
The set Q is the codomain of this relation.
Example 9. Let A = {1, 2} and B = {3, 4}. Find the number of relations from A to B.
Answer 9.
A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}.
Since n (A×B ) = 4, the number of subsets of A×B is 24
Therefore, the number of relations from A into B will be 24
Exercise 2.2 solved questions
Question 1. Let A = {1, 2, 3,…,14}. Define a relation R from A to A by R = {(x, y) : 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.
Answer 1.
R = { (1,3), (2,6), (3,9), (4,12) }
Domain of R = { 1,2,3,4 }
Co domain of R = A = {1, 2, 3,…,14}
Range of R = { 3,6,9,12 }
Question 2. Define a relation R on the set N of natural numbers by R = {(x, y) : y = x + 5, x is a natural number less than 4; x, y ∈N}. Depict this relationship using roster form. Write down the domain and the range.
Answer 2. R = { (1,6), (2,7), (3,8) }
Domain of R = {1,2,3}
Range of R = {6,7,8}
Question 3. A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}. Write R in roster form.
Answer 3. R = { (1,4), (1,6), (2,9), (3,4), (3,6), (5,4), (5,6) }
Question 4. The Fig 2.7 shows a relationship between the sets P and Q. Write this relation (i) in set-builder form (ii) roster form. What is its domain and range?
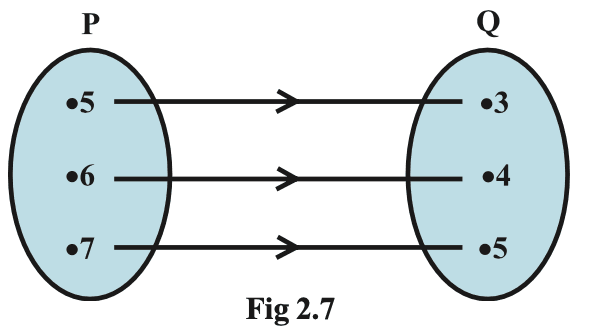
Answer 4.
(i) R = {(x, y) : y = x – 2, where x= 5,6,7}
(ii) R = { (5,3), (6,4), (7,5) }
Domain of R = { 5, 6, 7 }
Range of R = { 3, 4, 5 }
Question 5. Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a , b ∈A, b is exactly divisible by a}. (i) Write R in roster form (ii) Find the domain of R (iii) Find the range of R.
Answer 5.
(i) R = { (1,2), (1,3), (1,4), (1,6), (2,4), (2,6), (3,6), (1,1), (2,2), (3,3), (4,4), (6,6) }
(ii) Domain of R = {1, 2, 3, 4, 6}
(iii) Range of R = {1, 2, 3, 4, 6}
Question 6. Determine the domain and range of the relation R defined by R = {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}}
Answer 6.
R = { (0,5), (1,6), (2,7), (3,8), (4,9), (5,10) }
Domain of R = {0, 1, 2, 3, 4, 5}
Range of R = {5,6,7,8,9,10}
Question 7. Write the relation R = {(x, x3 ) : x is a prime number less than 10} in roster form
Answer 7.
x = { 2, 3, 5, 7 }
R = {(2,8), (3,27), (5,125), (7,343)}
Question 8. Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.
Answer 8. n(A) = 3, n(B) = 2
26 =64
Question 9. Let R be the relation on Z defined by R = {(a,b): a, b ∈ Z, a – b is an integer}. Find the domain and range of R.
Answer 9.
R = { (a,b) : a,b ∈ Z }
Domain of R = Z
Range of R = Z
