Last Updated:
Written by:
Time to read:
NCERT Exemplar Class 11 Maths Chapter 2 Relations and Functions Exercise Solutions Objective Type
Table of Contents
Solved Objective Type Questions of NCERT Exemplar Chapter 2 Relations and Functions Exercise
Question 24 Let n(A) = m and n(B) = n.
The total number of non-empty relations that can be defined from A to B is:
(a) mⁿ
(b) nᵐ − 1
(c) mn − 1
(d) 2ᵐⁿ − 1
Answer 24
A relation from A to B is a subset of A × B
Number of elements in A × B = mn
Total number of subsets of A × B = 2(mn)
Empty subset = ∅
Number of non-empty relations = 2(mn) − 1
Question 25
If [x]² − 5[x] + 6 = 0,
where [.] denotes the greatest integer function, then:
(a) x ∈ [3, 4]
(b) x ∈ (2, 3]
(c) x ∈ [2, 3]
(d) x ∈ [2, 4)
Answer 25
Let [x] = n, where n is an integer.
Given equation:
n² − 5n + 6 = 0
Factorising:
(n − 2)(n − 3) = 0
So,
n = 2 or n = 3
Case 1:
[x] = 2
⇒ 2 ≤ x < 3
Case 2:
[x] = 3
⇒ 3 ≤ x < 4
Combining both cases:
2 ≤ x < 4
So,
x ∈ [2, 4)
Correct option is (d)
Question 26. Range of f(x) = 1 / (1 − 2 cos x) is:
(a) [1/3, 1]
(b) [−1, 1/3]
(c) (−∞, −1] ∪ [1/3, ∞)
(d) [−1/3, 1]
Answer 26.
f(x) = 1 / (1 − 2 cos x)
We know that:
−1 ≤ cos x ≤ 1
⇒ −1 ≤ −2 cos x ≤ 2
⇒ −1 ≤ 1 − 2 cos x ≤ 3
Taking reciprocal (sign does not change as denominator ≠ 0):
−1 ≤ 1 / (1 − 2 cos x) ≤ 1/3
So,
Range of f(x) = [−1, 1/3]
Correct option:
(b)
Question 27. Let f(x) = √(1 + x²), then:
(a) f(xy) = f(x) f(y)
(b) f(xy) ≥ f(x) f(y)
(c) f(xy) ≤ f(x) f(y)
(d) None of these
Answer 27. f(x) = √(1 + x²)
f(xy) = √(1 + x²y²)
f(x) f(y) = √(1 + x²) √(1 + y²)
= √(1 + x² + y² + x²y²)
Since,
1 + x²y² ≤ 1 + x² + y² + x²y²
⇒ √(1 + x²y²) ≤ √(1 + x² + y² + x²y²)
⇒ f(xy) ≤ f(x) f(y)
Correct option:
(c)
Question 28. Domain of √(a² − x²), where a > 0, is:
(a) (−a, a)
(b) [−a, a]
(c) [0, a]
(d) (−a, 0]
Answer 28.
For √(a² − x²) to be defined,
a² − x² ≥ 0
⇒ x² ≤ a²
From x² ≤ a²
Taking square root on both sides:
|x| ≤ a
Removing modulus:
−a ≤ x ≤ a
⇒ −a ≤ x ≤ a
So, the domain is [−a, a]
Correct option:
(b)
Below is an example showing why modulus is converted to inequality
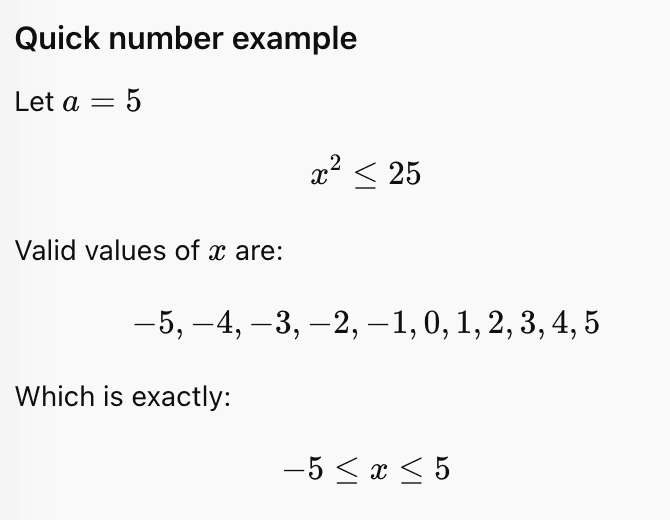
Question 29. If f(x) = ax + b, where a and b are integers,
f(−1) = −5 and f(3) = 3, then a and b are equal to:
(a) a = −3, b = −1
(b) a = 2, b = −3
(c) a = 0, b = 2
(d) a = 2, b = 3
Answer 29. f(x) = ax + b
f(−1) = −a + b = −5
⇒ a − b = 5 …(i)
f(3) = 3a + b = 3 …(ii)
Solving (i) and (ii):
a = 2
b = −3
Correct option:
(b)
Question 30. The domain of the function f defined by
f(x) = √(4 − x) + 1 / √(x² − 1) is equal to:
(a) (−∞, −1) ∪ (1, 4]
(b) (−∞, −1] ∪ (1, 4]
(c) (−∞, −1) ∪ [1, 4]
(d) (−∞, −1) ∪ [1, 4)
Answer 30.
f(x) is defined if both conditions are satisfied.
From √(4 − x):
4 − x ≥ 0
⇒ x ≤ 4
From 1 / √(x² − 1):
x² − 1 > 0
⇒ (x − 1)(x + 1) > 0
⇒ x < −1 or x > 1
Combining both conditions:
x < −1
or
1 < x ≤ 4
So, domain of f(x) is
(−∞, −1) ∪ (1, 4]
Correct option:
(a)
Question 31. The domain and range of the real function f defined by f(x) = (4 − x) / (x − 4) is given by
(a) Domain = R, Range = {−1, 1}
(b) Domain = R − {1}, Range = R
(c) Domain = R − {4}, Range = R − {−1}
(d) Domain = R − {−4}, Range = {−1, 1}
Answer 31.
Given that:
f(x) = (4 − x) / (x − 4)
We know that f(x) is defined if
x − 4 ≠ 0 ⇒ x ≠ 4
So, the domain of f(x) is:
R − {4}
Let
y = (4 − x) / (x − 4)
⇒ yx − 4y = 4 − x
⇒ yx + x = 4y + 4
⇒ x(y + 1) = 4(y + 1)
⇒ x = 4(1 + y) / (1 + y)
If x is a real number, then
1 + y ≠ 0 ⇒ y ≠ −1
∴ Range of f(x) = R − {−1}
Hence, the correct option is (c).
Question 32. The domain and range of real function f defined by
f(x) = √(x − 1) is given by
(a) Domain = (1, ∞), Range = (0, ∞)
(b) Domain = [1, ∞), Range = (0, ∞)
(c) Domain = [1, ∞), Range = [0, ∞)
(d) Domain = [1, ∞], Range = [0, ∞]
Answer 32. Given:
f(x) = √(x − 1)
Step 1: Domain
For a square-root function, the expression inside the root must be greater than or equal to zero.
x − 1 ≥ 0
⇒ x ≥ 1
Domain:
[1, ∞)
Step 2: Range
The square root of any non-negative number is always non-negative.
So,
f(x) ≥ 0
Range:
[0, ∞)
Final Answer
• Domain: [1, ∞)
• Range: [0, ∞)
Correct option: (c)
Question 33. The domain of the function f given by
f(x) = (x² + 2x + 1) / (x² − x − 6) is
(a) R − {3, −2}
(b) R − {−3, 2}
(c) R − {3, −2}
(d) R − (3, −2)
Answer 33.
Given that:
f(x) = (x² + 2x + 1) / (x² − x − 6)
f(x) is defined if
x² − x − 6 ≠ 0
⇒ x² − 3x + 2x − 6 ≠ 0
⇒ (x − 3)(x + 2) ≠ 0
⇒ x ≠ −2, x ≠ 3
So, the domain of f(x) = R − {−2, 3}
Hence, the correct option is (a)
Question 34. The domain and range of the function f given by
f(x) = 2 − |x − 5| is
(a) Domain = R⁺, Range = (−∞, 1]
(b) Domain = R, Range = (−∞, 2]
(c) Domain = R, Range = (−∞, 2)
(d) Domain = R⁺, Range = (−∞, 2]
Answer 34.
Given that:
f(x) = 2 − |x − 5|
Here, f(x) is defined for x ∈ R
∴ Domain of f(x) = R
Now,
|x − 5| ≥ 0
⇒ −|x − 5| ≤ 0
⇒ 2 − |x − 5| ≤ 2
⇒ f(x) ≤ 2
∴ Range of f(x) = (−∞, 2]
Hence, the correct option is (b)
Question 35. The domain for which the functions defined by
f(x) = 3x² − 1
and
g(x) = 3 + x
are equal is
(a) {−1, 4/3}
(b) {−1, 4/3}
(c) {−1, 4/3}
(d) {−1, 4/3}
Answer 35.
Given that:
f(x) = 3x² − 1 and g(x) = 3 + x
f(x) = g(x)
⇒ 3x² − 1 = 3 + x
⇒ 3x² − x − 4 = 0
⇒ 3x² − 4x + 3x − 4 = 0
⇒ x(3x − 4) + 1(3x − 4) = 0
⇒ (x + 1)(3x − 4) = 0
⇒ x + 1 = 0 or 3x − 4 = 0
⇒ x = −1 or x = 4/3
∴ Domain = {−1, 4/3}
Hence, the correct option is (a).
