Real Numbers

Understand concepts involved in topic real numbers

Last updated : 13 June 2024, Thursday

Verified for accuracy

Definitions and Examples in Real Numbers

Real Numbers: Real numbers are a set of numbers that includes all rational and irrational numbers. They can be represented on the number line and include integers, fractions, decimals, and more. Real numbers are the most comprehensive set of numbers in mathematics.

Rational Numbers:
- Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers, and q is not equal to zero. In other words, rational numbers are those that can be written as the ratio of two integers. Examples include 1/2, -3/4, and 5.
- p and q are co-prime, that means they do not have common factors other than 1
- Rational Numbers do not have unique representation in form p/q , for example, 1/2 can be represented as 2/4, 10/20, 25/50 and so on, these are equivalent rational numbers or fractions
- To find rationals numbers between p and q, you can add p and q and divide the sum by 2, means (p+q)/2 lies between p and q. Let us say new number is ‘r’, then add r and q and divide sum by 2 so that the new number lies between p and q. Repeat the procedures to find more numbers between p and q.
- There are infinitely many rational numbers between any two given rational numbers.

Irrational Numbers: Irrational numbers are numbers that cannot be expressed as a fraction of two integers. They have non-repeating, non-terminating decimal expansions. Common examples include the square root of 2 (√2), π (pi), and e (Euler’s number). They are represented by Q’
Integers: Integers are whole numbers, both positive and negative, as well as zero. They do not include fractions or decimal points. Integers include numbers like -3, -2, -1, 0, 1, 2, 3, and so on. They are represented by Z
Whole Numbers: Whole numbers are a subset of integers that include all the positive integers (1, 2, 3, …) and zero (0). They do not include negative numbers. They are represented by W
Natural Numbers: Natural numbers, also known as counting numbers, are a subset of whole numbers that begin at 1 and continue indefinitely (1, 2, 3, …). Natural numbers are used for counting and ordering. They are represented by N
Imaginary numbers and infinity are not real numbers

Locating irrational numbers on number line

Perform the below activity to know how √2, √3 and other irrational numbers are represented on the number line

Perform Activity

Proving √2 is irrational number

To prove that √2 is irrational, we can use a proof by contradiction. This method involves assuming the opposite of what we want to prove, showing that this assumption leads to a contradiction, and then concluding that the original statement must be true. Here’s how the proof goes:

Assumption: Assume that √2 is rational. By definition, a rational number can be expressed as a fraction a/b , where a and b are integers, and b not equal to 0. Additionally, we can assume that this fraction is in its simplest form, meaning a and b have no common
factors other than 1.
Expressing √2: Based on our assumption, we can write √2 = a/b Squaring both sides of the equation gives 2 = a²/b² or a²=2b²
Implication of the Equation: Since a²=2b², it implies that a² is even (because it’s twice some integer). If a² is even, then a itself must also be even (only even numbers squared yield even results). So, we can write a as 2k for some integer k.
Substituting a: Substituting a = 2k into the equation a² = 2b² gives 2k² = 2b². Simplifying, we get 4k² = 2b², and then 2k² = b².
Contradiction: Now, since 2k²=b², it follows that b² is also even, which means b must be even. However, this is a contradiction to our original assumption that a and b have no common factors other than 1. If both a and b are even, they are both divisible by 2, which means they had a common factor.

Conclusion: Since our assumption that √2 is rational leads to a contradiction, we must conclude that √2 is irrational.

Square root spiral

How to construct segments whose lengths are irrational number? The spiral of Theodorus is a construction of continuous right triangles into a spiral. Each right triangle has a side length of one unit.

Square root Spiral

Place Value

Each place in a number has a different value called its place value. A place value chart is a useful way to summarize this information. The place values are separated into groups of three, called periods. The periods are ones, thousands, millions, billions, trillions, and so on. In a written number, commas separate the periods.

Place Value Chart and writing place value

Using Place Value to Name Whole Numbers

Step 1. Starting at the digit on the left, name the number in each period, followed by the period name. Do not include the period name for the ones.

Step 2. Use commas in the number to separate the periods.

The number is eight trillion, one hundred sixty-five billion, four hundred thirty-two million, ninety-eight thousand, seven hundred ten.

Using place value to Write Whole Numbers

Writing numbers given in words as digits:

Step 1. Identify the words that indicate periods. (Remember the ones period is never named.)

Step 2. Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.

Step 3. Name the number in each period and place the digits in the correct place value position.

Example : fifty-three million, four hundred one thousand, seven hundred forty-two

Identify the words that indicate periods.

Except for the first period, all other periods must have three places. Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.

Then write the digits in each period.

Using place value to Write Whole Numbers

Put the numbers together, including the commas. The number is 53,401,742

How to round a whole number to a specific place value?

Step 1. Locate the given place value. All digits to the left of that place value do not change unless the digit immediately to the left is 9, in which case it may. (See Step 3.)

Step 2. Underline the digit to the right of the given place value.

Step 3. Determine if this digit is greater than or equal to 5.

Yes—add 1 to the digit in the given place value. If that digit is 9, replace it with 0 and add 1 to the digit immediately to its left. If that digit is also a 9, repeat.
No—do not change the digit in the given place value.

Step 4. Replace all digits to the right of the given place value with zeros.

Properties of Real Numbers

The properties of real numbers are fundamental concepts in mathematics, especially in algebra. These properties are used to perform operations and solve equations involving real numbers. Here’s a brief overview of the key properties:

1. Commutative Property: This property applies to addition and multiplication. It states that the order of the numbers does not change the result. For example, a + b = b + a and ab = ba.

2. Associative Property: This property also applies to addition and multiplication. It indicates that the way numbers are grouped does not affect the sum or product. For example, (a + b) + c = a + (b + c) and (ab)c = a(bc)

3. Distributive Property: This property links addition and multiplication. It states that multiplying a sum by a number is the same as multiplying each addend by the number and then adding the products. For example, a(b + c) = ab + ac

4. Identity Property: There are two types of identity properties: Additive Identity: The sum of any number and zero is the number itself. For example, a + 0 = a

– Multiplicative Identity: The product of any number and one is the number itself. For example, a × 1 = a

5. Inverse Property: This property also comes in two forms:

– Additive Inverse: The sum of a number and its opposite (negative) is zero. For example, a + (-a) = 0

– Multiplicative Inverse: The product of a number and its reciprocal is one. For example, a times 1/a = 1 (assuming a is not zero)

6. Closure Property: This property states that the sum or product of any two real numbers is a real number. For example, if a and b are real, then a + b and ab are also real.

7. Zero Product Property: If the product of two real numbers is zero, then at least one of the factors must be zero. For example, if ab = 0, then either a = 0 or b = 0 or both.

8. Transitive Property: If two numbers are equal to the same number, then they are equal to each other. For example, if a = b and b = c, then a = c

9. Symmetric Property: If one number is equal to another, then the second is equal to the first. For example, if a = b, then b = a.

10. Reflexive Property: Each number is equal to itself. For example, a = a

These properties are the building blocks for solving equations and understanding algebraic structures in mathematics. They apply not only to simple numbers but also to more complex expressions involving variables.

Real Numbers and their decimal expansions

The decimal expansion of a rational number is either terminating or non-terminating recurring. Moreover, a number whose decimal expansion is terminating or non-terminating recurring is rational.

The decimal expansion of an irrational number is non-terminating non-recurring. Moreover, a number whose decimal expansion is non-terminating non-recurring is irrational.

Non terminating but repeating decimals

Non-terminating but repeating decimals are decimal representations of rational numbers that, when divided out, result in a repeating pattern of digits after the decimal point. These numbers are often denoted with a bar over the repeating part. The repeating part of the decimal continues indefinitely, even though it’s a finite sequence of digits that repeats over and over. These are also known as “recurring decimals.”

For example, the decimal representation of the fraction 1/3 is a non-terminating but repeating decimal:1/3 = 0.3333… (with the 3’s repeating indefinitely) Another common example is 1/7: 1/7 = 0.142857142857… (with the sequence “142857” repeating indefinitely)

In general, any fraction p/q, where p and q are integers and q is not divisible by any prime other than 2 or 5 (in the denominator) will result in a non-terminating but repeating decimal when expressed in decimal form.

These non-terminating but repeating decimals are a subset of rational numbers, as they can be expressed as fractions (ratios of integers), but their decimal representations exhibit a repeating pattern of digits after the decimal point.

Operations on Real Numbers

The sum or difference of a rational number and an irrational number is irrational.
The product or quotient of a non-zero rational number with an irrational number is irrational
If we add, subtract, multiply or divide two irrationals, the result maybe rational or irrational

Prime, Composite, Even, Odd Numbers

Prime Numbers : Prime numbers are natural numbers greater than 1 that are only divisible by 1 and themselves. Examples include 2, 3, 5, 7, and 11.
Composite Numbers: Composite numbers are natural numbers greater than 1 that have more than two distinct positive divisors. In other words, they are not prime.
Even Numbers: Even numbers are integers that are divisible by 2, meaning they have no remainder when divided by 2 (e.g., -4, -2, 0, 2, 4, …).
Odd Numbers: Odd numbers are integers that are not divisible by 2, meaning they have a remainder of 1 when divided by 2 (e.g., -3, -1, 1, 3, 5, …).

Complex and Imaginary Numbers

Complex numbers are numbers of the form a + bi, where “a” and “b” are real numbers, and “i” is the imaginary unit, defined as the square root of -1.
Imaginary numbers are numbers in the form of ai, where “a” is a real number, and “i” is the imaginary unit. They are used in complex numbers.

Square Root of positive real numbers geometrically

For example, find the square root of 3.5 geometrically

x is 3.5
Draw a line AB of length x=3.5. From the point B, draw a line of 1 unit, where the length of BC=1
Find the mid-point of AC and mark it D. Draw a semicircle with center D and radius AD. Draw a line perpendicular to AC passing through B and intersecting the semicircle at E.
Then BE is square root of 3.5

Finding root 2 plus root 5

Applications of Real Numbers

A) Real numbers are fundamental in mathematics and have a wide range of applications across various fields. Here are some key applications of real numbers:

1. Science and Engineering

Measurements: Real numbers are used to measure quantities such as length, mass, temperature, and time.
Physics: Real numbers are essential in formulating physical laws and equations, such as Newton’s laws of motion, the equations of thermodynamics, and quantum mechanics.
Engineering: Real numbers are used in calculations involving electrical circuits, structural analysis, fluid dynamics, and other engineering fields.

2. Finance and Economics

Currency and Prices: Real numbers represent money, prices, interest rates, and other financial metrics.
Statistics and Econometrics: Real numbers are used in data analysis, regression models, and economic forecasting.

3. Computer Science

Algorithms: Real numbers are used in algorithms for data processing, graphics rendering, and machine learning.
Simulations: Real numbers are used in simulations and modeling of real-world phenomena, including climate models and traffic systems.

4. Everyday Life

Cooking and Baking: Real numbers are used in recipes for measuring ingredients.
Travel: Real numbers are used in calculating distances, speeds, and travel times.
Sports: Real numbers are used to record times, distances, scores, and other metrics.

5. Medicine and Biology

Dosage Calculations: Real numbers are used to determine the appropriate dosage of medications.
Statistical Analysis: Real numbers are used in analyzing medical data, clinical trials, and genetic research.

6. Commerce and Trade

Pricing and Discounts: Real numbers are used to calculate prices, discounts, and taxes.
Inventory Management: Real numbers are used in tracking quantities of goods and optimizing stock levels.

7. Education

Grading and Assessment: Real numbers are used to score exams, calculate grades, and analyze educational data.
Research: Real numbers are used in academic research for statistical analysis and hypothesis testing.

8. Art and Design

Graphics and Animation: Real numbers are used in the creation of digital graphics, animation, and visual effects.
Music: Real numbers are used in the tuning of musical instruments and the analysis of sound waves.

9. Astronomy and Space Exploration

Distance Measurements: Real numbers are used to measure astronomical distances and calculate orbital paths.
Time Calculations: Real numbers are used in determining time intervals and synchronizing space missions.

10. Geography and Cartography

Mapping: Real numbers are used in creating maps and determining geographical coordinates.
Topography: Real numbers are used in measuring elevations and describing terrain features.

Real numbers form the basis of many mathematical concepts and are integral to the functioning of numerous scientific, engineering, economic, and everyday applications.

B) Real numbers are versatile and play a crucial role in various applications. As you delve into the practical aspects of working with real numbers, you’ll find that they provide a solid foundation for understanding and solving problems in different contexts:

Arithmetic Operations and PEMDAS:
- When tackling real-world problems, mastering the order of operations becomes essential. From calculating expenses to solving complex equations, understanding PEMDAS ensures accuracy in your computations.
Representation with Fractions and Decimals:
- Real numbers extend beyond whole numbers, offering precision in representing quantities. Explore how fractions and decimals contribute to a nuanced understanding of numerical values.
Percentage Calculations and Percents:
- Real numbers seamlessly integrate with percentages in practical scenarios. Whether you’re calculating discounts or interpreting growth rates, a solid grasp of percents enhances your ability to work with real-world data.
Comparisons and Ratios:
- Ratios, expressions of relationships between quantities, are fundamental in real-world applications. Real numbers provide the foundation for making meaningful comparisons and understanding ratios in diverse contexts.
Proportional Relationships and Proportions:
- Real numbers are instrumental in expressing proportional relationships. Whether you’re scaling recipes, understanding financial ratios, or solving engineering problems, proportions help maintain balance and consistency
Prime Factorization:
- Explore the concept of prime factorization and its significance in breaking down numbers into their prime components. This technique is valuable in various mathematical and problem-solving scenarios.
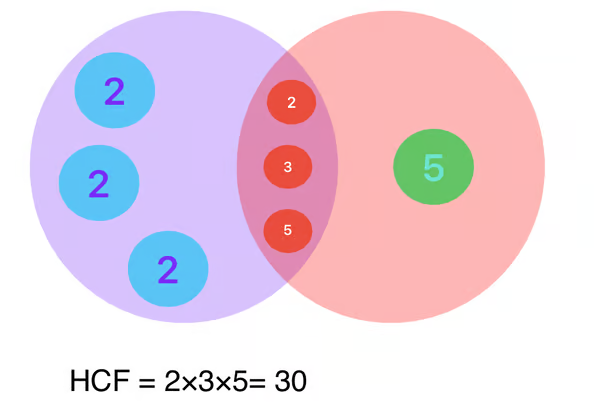
HCF and LCM:
- Real numbers play a crucial role in determining the HCF (Highest Common Factor) and LCM (Least Common Multiple) of sets of numbers. These concepts are essential in tasks ranging from simplifying fractions to time management calculations.