Prime Factorization

Introduction

Prime factorization is a fundamental concept in mathematics that involves breaking down a number into its prime components. It serves as the foundation for various mathematical and computational algorithms, making it an essential skill for students and enthusiasts. In this article, we will delve into the world of prime factorization, exploring its significance, methods, and real-world applications. Prime factorization involves expressing a given integer as a product of its prime factors. This process not only provides a unique representation of the number but also allows for a deeper understanding of its mathematical properties.

Factors and Multiples

A factor is a term used in mathematics to describe a number or expression that can be evenly divided into another number or expression without leaving a remainder.

A multiple is a number that can be evenly divided by another number. In other words, when one number is a multiple of another, it means that the first number can be obtained by multiplying the second number by an integer (a whole number).

Methods of prime factorisation

1. Trial Division Method

• The trial division method involves dividing the number by progressively larger prime numbers.
• Start with the smallest prime number (2) and continue to divide until the number is no longer divisible by the current prime.
• Record each prime factor and continue with the quotient until it becomes 1.

For example, let’s find the prime factors of 36 using trial division:

• Start with 2: 36 ÷ 2 = 18
• Continue with 2: 18 ÷ 2 = 9
• Continue with 3: 9 ÷ 3 = 3
• Continue with 3: 3 ÷ 3 = 1

The prime factors of 36 are 2 and 3

2. Prime Factorisation Tree

• Another method involves constructing a factorization tree, which visually represents the prime factors of a number.
• Start by dividing the number by its smallest prime factor and write down the quotient.
• Continue this process for each quotient until you reach 1, and then collect all the prime factors from the tree.

Applications

Prime factorization has numerous practical applications in mathematics, computer science, and cryptography. Here are a few areas where it plays a crucial role:

1. Cryptography: Prime factorization is at the heart of encryption techniques like RSA (Rivest-Shamir-Adleman). The security of these systems relies on the difficulty of factoring the product of two large prime numbers.
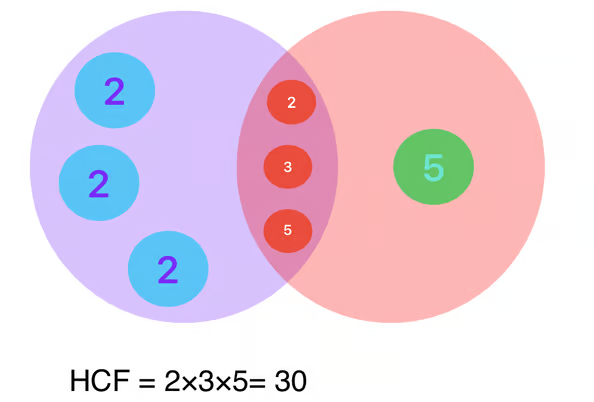
2. Number Theory: Prime factorization is an essential tool for solving various problems in number theory, such as finding the greatest common divisor (GCD) and the least common multiple (LCM) of numbers.
3. Algorithms: Prime factorization algorithms are used in computer science for tasks like simplifying fractions, reducing fractions to their lowest terms, and solving diophantine equations.
4. Computational Mathematics: In computational mathematics, prime factorization is used in tasks like integer factorization, which has applications in solving complex mathematical problems and simulating physical systems.

Quiz