HCF and LCM

Introduction

HCF (Highest Common Factor) and LCM (Lowest Common Multiple) are fundamental concepts in mathematics that play a crucial role in various mathematical operations and problem-solving. They are particularly important in number theory, algebra, and many real-world applications. In this article, we will delve into these two concepts, exploring their definitions and their calculation methods.

HCF

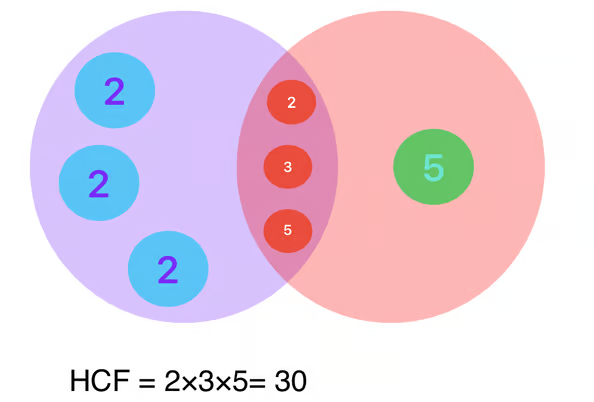
HCF, also known as GCD (Greatest Common Divisor), is the largest positive integer that divides two or more given numbers without leaving a remainder. It represents the highest factor that is common to all the numbers in question. The HCF is an essential concept in simplifying fractions and solving problems related to ratios, proportions, and divisibility.

Prime Factorisation Method to find HCF of 2 or more numbers

• Express each number as a product of its prime factors.
• Identify the common prime factors and find the smallest exponent for each common factor.
• Multiply the common prime factors with the smallest exponent to obtain the HCF.

Division method to find HCF of 2 numbers:

• Divide the larger number by the smaller one.
• Replace the larger number with the smaller one and the smaller number with the remainder obtained.
• Repeat this process until the remainder becomes zero.
• The divisor at this point is the HCF of the two numbers.

Division method to find HCF of more than 2 numbers:

• Start by finding the HCF of the first two numbers using the division method, as explained earlier.
• Once you have the HCF of the first two numbers, you can then find the HCF of this result and the next number.
• Repeat this process for each additional number, using the HCF obtained in the previous step along with the next number, until you have gone through all the numbers.
• The final result is the HCF of all the numbers.

• LCM, also known as the least common multiple, is the smallest positive integer that is a multiple of two or more given numbers. It represents the smallest number at which the given numbers have a common multiple. LCM is frequently used in applications such as finding a common denominator for fractions and solving problems related to time, distance, and periodic events.
• To calculate the LCM of two or more numbers, you can use various methods, including the prime factorization method, listing multiples, and the division method. Here, we will discuss the prime factorization method:
• A) Express each number as a product of its prime factors.

B) Identify all unique prime factors among these numbers.

C) Calculate the LCM by multiplying these unique prime factors with their highest exponents

Quiz