Chapter 2 Relations and Functions

Ordered Pair Definition

An ordered pair of elements taken from any two sets P and Q is a pair of elements written in small brackets and grouped together in a particular order, i.e., (p,q), p ∈ P and q ∈ Q

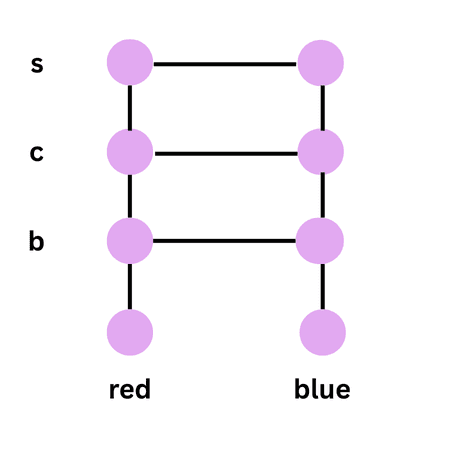
For example, suppose A is a set of 2 colours and B is a set of 3 objects, i.e., A = {red, blue} and B = {b, c, s}, where b, c and s represent a particular bag, coat and shirt, respectively, then, Ordered Pairs of coloured objects that can be made from these two sets are:

(red, b), (red, c), (red, s), (blue, b), (blue, c), (blue, s)

Cartesian Product of Sets

Given two non-empty sets P and Q. The cartesian product P × Q is the set of all ordered pairs of elements from P and Q, i.e., P × Q = { (p,q) : p ∈ P, q ∈ Q }

Above sentence simply means:

P × Q is the set of all ordered pairs (p, q) where the first element p is taken from set P and the second element q is taken from set Q.

In other words, we choose one element from P and one element from Q and write them in order as (p, q). All such ordered pairs together form the Cartesian product P × Q.

If either P or Q is the null set, then P × Q will also be empty set, i.e., P × Q = φ

Remarks

1. Two ordered pairs are equal, if and only if the corresponding first elements are equal and the second elements are also equal.
2. If there are p elements in A and q elements in B, then there will be pq elements in A × B, i.e., if n(A) = p and n(B) = q, then n(A × B) = pq
3. If A and B are non-empty sets and either A or B is an infinite set, then so is A × B.
4. A × A × A = {(a, b, c) : a, b, c ∈ A}. Here (a, b, c) is called an ordered triplet. Means the set of all ordered triplets where each of the three entries is taken from set A.

Examples of Cartesian Product of Sets

Example 1

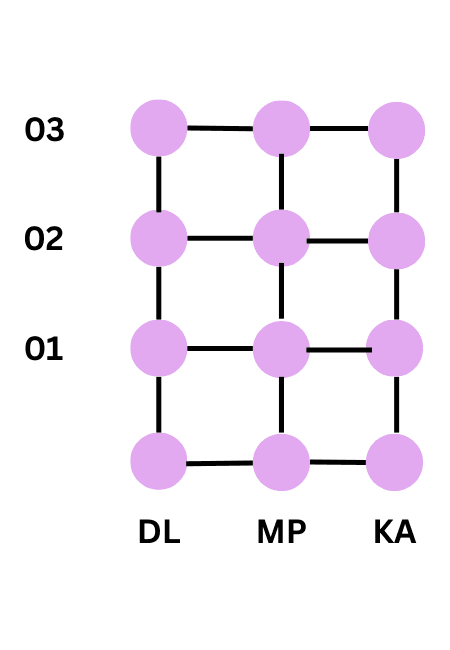
Consider the two sets: A = {DL, MP, KA}, where DL, MP, KA represent Delhi, Madhya Pradesh and Karnataka, respectively B = {01,02,03} representing codes for the licence plates of vehicles issued by DL, MP and KA. If the three states, Delhi, Madhya Pradesh and Karnataka were making codes for the licence plates of vehicles, with the restriction that the code begins with an element from set A, which are the pairs available from these sets then the available pairs are:(DL,01), (DL,02), (DL,03), (MP,01), (MP,02), (MP,03), (KA,01), (KA,02), (KA,03) and the product of set A and set B is given by A × B = {(DL,01), (DL,02), (DL,03), (MP,01), (MP,02), (MP,03), (KA,01), (KA,02), (KA,03)}. It can easily be seen that there will be 9 such pairs in the Cartesian product, since there are 3 elements in each of the sets A and B. This gives us 9 possible codes. Also note that the order in which these elements are paired is crucial. For example, the code (DL, 01) will not be the same as the code (01, DL).

Example 2

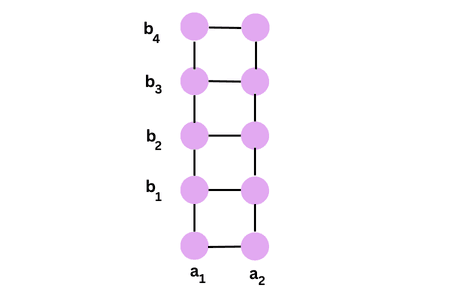
Consider the two sets A= {a₁ , a₂ } and B = {b₁ , b₂ , b₃ , b₄ } .

A × B = {( a₁ , b₁ ), (a₁ , b₂ ), (a₁ , b₃ ), (a₁ , b₄ ), (a₂ , b₁ ), (a₂ , b₂ ), (a₂ , b₃ ), (a₂ , b₄ )}.

The 8 ordered pairs thus formed can represent the position of points in the plane if A and B are subsets of the set of real numbers and it is obvious that the point in the position (a₁ , b₂ ) will be distinct from the point in the position (b₂ , a₁ ).

Relations, Image, Domain, Codomain

A relation R from a non-empty set A to a non-empty set B is a subset of the cartesian product A × B. The subset is derived by describing a relationship between the first element and the second element of the ordered pairs in A × B. The second element is called the image of the first element

The set of all first elements of the ordered pairs in a relation R from a set A to a set B is called the domain of the relation R.

The set of all second elements in a relation R from a set A to a set B is called the range of the relation R. The whole set B is called the codomain of the relation R. Note that range ⊂ codomain.

A relation may be represented algebraically either by the Roster method or by the Set-builder method. An arrow diagram is a visual representation of a relation.

A relation R from A to A is also stated as a relation on A.

Example of a relation

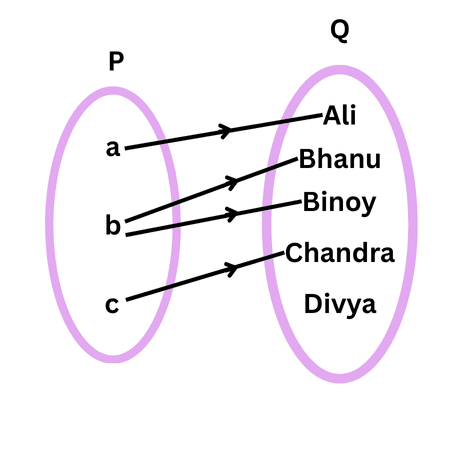
Consider the two sets P= {a, b, c} and Q = {Ali, Bhanu, Binoy, Chandra, Divya}.

The cartesian product of P and Q has 15 ordered pairs which can be listed as P × Q = {(a, Ali), (a, Bhanu), (a, Binoy), …, (c, Divya)}.

We can now obtain a subset of P x Q by introducing a relation R between the first element x and the second element y of each ordered pair (x,y) as

R = { (x,y) : x is the first letter of the name y, x ϵ P, y ϵ Q }

Then, R = { (a, Ali), (b, Bhanu), (b, Binoy), (c, Chandra) }

A visual representation of this relation R (called an arrow diagram) is shown in the image

The total number of relations that can be defined from a set A to a set B is the number of possible subsets of A × B. If n(A) = p and n(B) = q, then

n (A x B) = pq and the total number of relations is 2^pq

Functions

A relation f from a set A to a set B is said to be a function if every element of set A has one and only one image in set B.

In other words, a function f is a relation from a non-empty set A to a non-empty set B such that the domain of f is A and no two distinct ordered pairs in f have the same first element. If f is a function from A to B and (a, b) ∈ f, then f (a) = b, where b is called the image of a under f and a is called the preimage of b under f.

The function f from A to B is denoted by f: A → B

Real valued function and real function

A function which has either R or one of its subsets as its range is called a real valued function. Further, if its domain is also either R or a subset of R, it is called a real function.

Some functions and their graphs

(i) Identity Function :

Let R be the set of real numbers. Define the real valued function f : R → R by y = f(x) = x for each x ∈ R. Such a function is called the identity function. Here the domain and range of f are R. The graph is a straight line. It passes through the origin

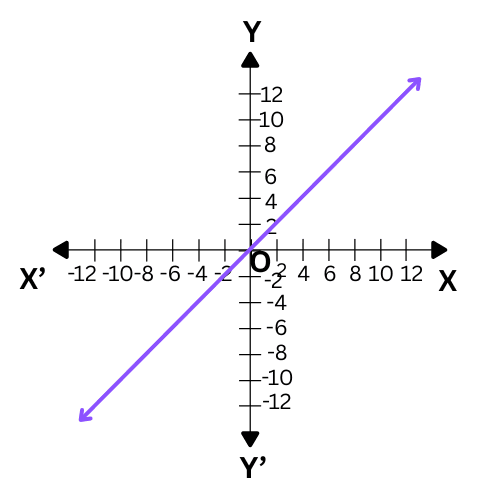
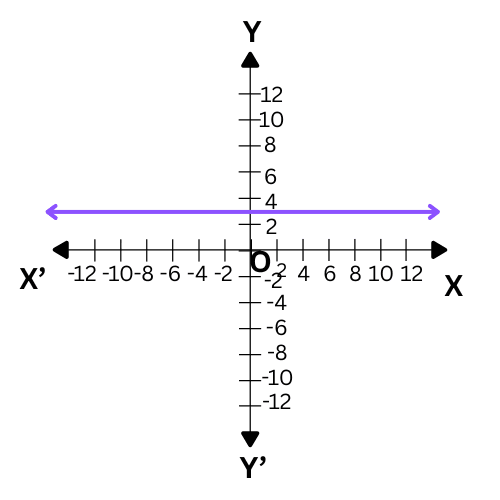
(ii) Constant Function :

Define the function f: R → R by y = f (x) = c, x ∈ R where c is a constant and each x ∈ R. Here domain of f is R and its range is {c}. The graph is a line parallel to x-axis. For example, if f(x)=3 for each x∈R

(iii) Polynomial Function:

A function f : R → R is said to be polynomial function if for each x in R, y = f (x) = a₀ + a₁ x + a₂ x² +…a_n xⁿ , where n is a non-negative integer and a₀, a₁, a₂,…a_n 𝛜 R

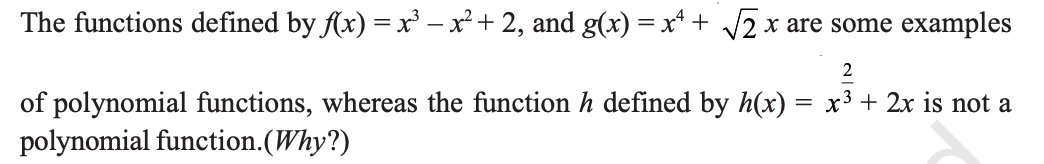
(iv) Rational Functions:

Rational functions are functions of the type f(x)/g(x), where f(x) and g(x) are polynomial functions of x defined in a domain, where g(x) ≠ 0

(v) Modulus Function:

The function f: R→R defined by f(x) = |x| for each x ∈R is called modulus function. For each non-negative value of x, f(x) is equal to x.

But for negative values of x, the value of f(x) is the negative of the value of x, i.e.,

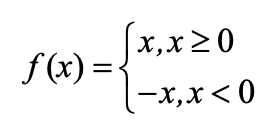
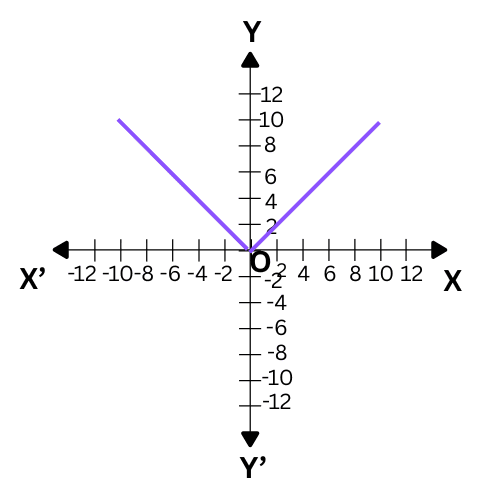
(vi) Signum Function:

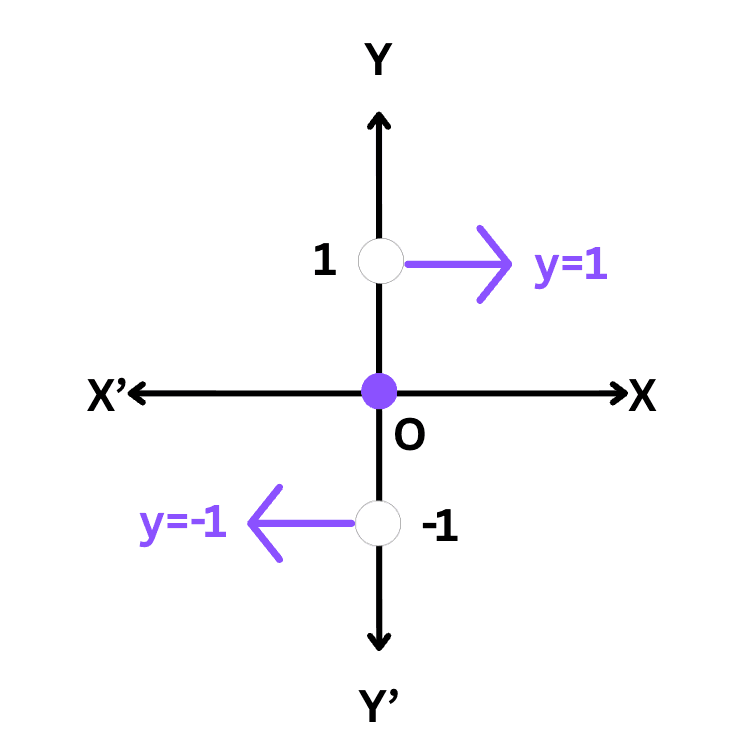
The function f:R→R defined by:

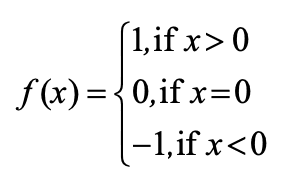
is called the signum function. The domain of the signum function is R and the range is the set {–1, 0, 1}.

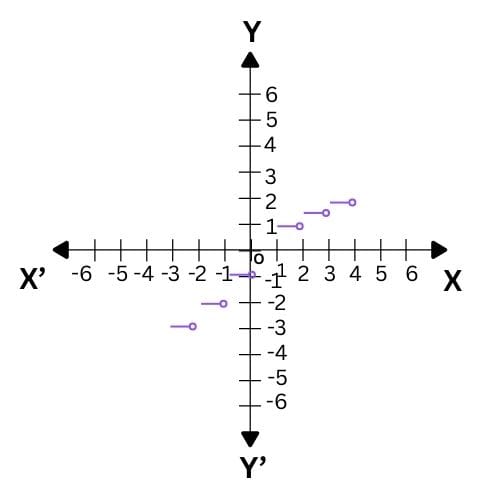
(vii) Greatest Integer Function:

The function f: R → R defined by f(x) = [x], x ∈R assumes the value of the greatest integer, less than or equal to x. Such a function is called the greatest integer function. From the definition of [x], we can see that
[x] = –1 for –1 ≤ x < 0
[x] = 0 for 0 ≤ x < 1
[x] = 1 for 1 ≤ x < 2
[x] = 2 for 2 ≤ x < 3 and so on

Algebra of real functions

(i) Addition of two real functions : Let f : X → R and g : X → R be any two real functions, where X ⊂ R. Then, we define (f + g): X → R by (f + g) (x) = f (x) + g (x), for all x ∈ X.

(ii) Subtraction of a real function from another : Let f : X → R and g: X → R be any two real functions, where X ⊂ R. Then, we define (f – g) : X→R by (f–g) (x) = f(x) – g(x), for all x ∈ X.

(iii) Multiplication by a scalar : Let f : X→R be a real valued function and α be a scalar. Here by scalar, we mean a real number. Then the product α f is a function from X to R defined by (α f ) (x) = α f (x), x ∈X.

(iv) Multiplication of two real functions : The product (or multiplication) of two real functions f:X→R and g:X→R is a function fg:X→R defined by (fg) (x) = f(x) g(x), for all x ∈ X.

This is also called pointwise multiplication.

(v) Quotient of two real functions : Let f and g be two real functions defined from X→R, where X ⊂ R.

The quotient of f by g denoted by f/g is a function defined by,