Written by : Anmol Gupta
8 mins read time
NCERT Exemplar Class 11 Maths Chapter 1 Sets Exercise Solutions Long Answer Type
Table of Contents
Solved Long Answer Type Questions of NCERT Exemplar Sets Exercise
Question 23 Let A, B and C be sets. Then show that
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Answer 23 To Prove:
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
We will prove this by double inclusion.
1. Show that:
A ∩ (B ∪ C) ⊂ (A ∩ B) ∪ (A ∩ C)
Let x ∈ A ∩ (B ∪ C)
This means:
- x ∈ A
- and x ∈ B ∪ C ⇒ x ∈ B or x ∈ C
Case 1: If x ∈ B, then x ∈ A ∩ B
Case 2: If x ∈ C, then x ∈ A ∩ C
In both cases, x ∈ (A ∩ B) ∪ (A ∩ C)
So,
A ∩ (B ∪ C) ⊂ (A ∩ B) ∪ (A ∩ C)
2. Show that:
(A ∩ B) ∪ (A ∩ C) ⊂ A ∩ (B ∪ C)
Let x ∈ (A ∩ B) ∪ (A ∩ C)
This means:
- x ∈ A ∩ B or x ∈ A ∩ C
Case 1: If x ∈ A ∩ B, then x ∈ A and x ∈ B ⇒ x ∈ B ∪ C
Case 2: If x ∈ A ∩ C, then x ∈ A and x ∈ C ⇒ x ∈ B ∪ C
So in both cases, x ∈ A and x ∈ B ∪ C
Therefore, x ∈ A ∩ (B ∪ C)
Thus,
(A ∩ B) ∪ (A ∩ C) ⊂ A ∩ (B ∪ C)
Since both inclusions hold, we have:
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Question 24 Out of 100 students; 15 passed in English, 12 passed in Mathematics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science; 4 in English and Science; 4 in all the three. Find how many passed
(i) in English and Mathematics but not in Science
(ii) in Mathematics and Science but not in English
(iii) in Mathematics only
(iv) in more than one subject only
Answer 24.
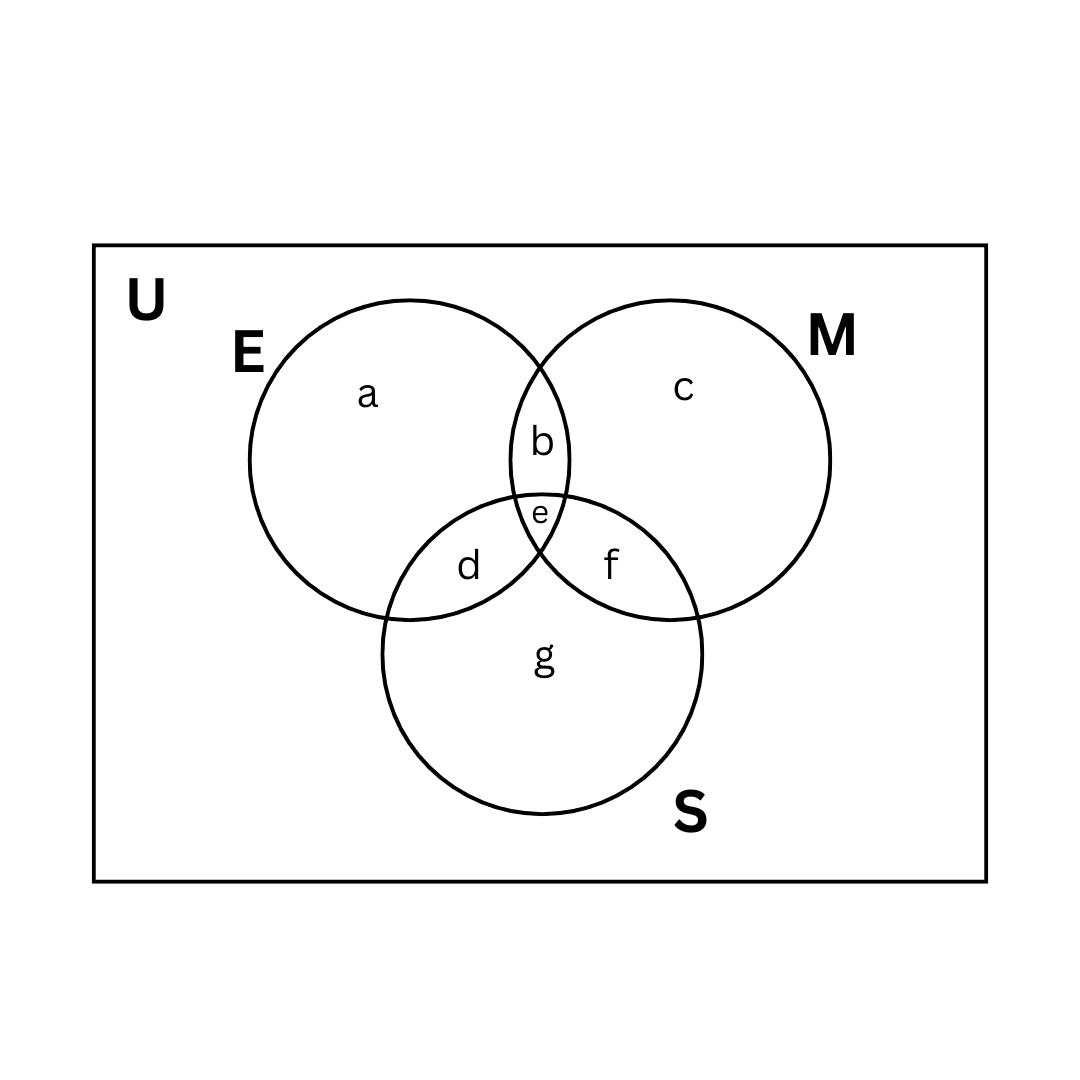
Let the number of students who passed in Mathematics be M, in English be E, and in Science be S.
Then
n(U) = 100, n(M) = 12,
n(E) = 15, n(S) = 8,
n(E ∩ M) = 6,
n(M ∩ S) = 7,
n(E ∩ S) = 4,
n(E ∩ M ∩ S) = 4
Let us draw a Venn diagram. According to the Venn diagram, we get:
a + b + d + e = 15 …(i)
b + c + e + f = 12 …(ii)
d + e + f + g = 8 …(iii)
From the information:
- n(E ∩ M) = 6, so b + e = 6 …(iv)
- n(M ∩ S) = 7, so e + f = 7 …(v)
- n(E ∩ S) = 4, so d + e = 4 …(vi)
- n(E ∩ M ∩ S) = 4, so e = 4 …(vii)
Now, solving step by step:
From eqn. (iv) and (vii):
b + 4 = 6 ⇒ b = 2
From eqn. (v) and (vii):
4 + f = 7 ⇒ f = 3
From eqn. (vi) and (vii):
d + 4 = 4 ⇒ d = 0
From eqn. (i):
a + b + d + e = 15 ⇒ a + 2 + 0 + 4 = 15 ⇒ a = 9
From eqn. (ii):
b + c + e + f = 12 ⇒ 2 + c + 4 + 3 = 12 ⇒ c = 3
From eqn. (iii):
d + e + f + g = 8 ⇒ 0 + 4 + 3 + g = 8 ⇒ g = 1
Final Answers:
(i) Number of students who passed in English and Mathematics but not in Science: b = 2
(ii) Number of students who passed in Mathematics and Science but not in English: f = 3
(iii) Number of students who passed in Mathematics only: c = 3
(iv) Number of students who passed in more than one subject = b + e + d + f = 2 + 4 + 0 + 3 = 9
Question 25. In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Find the number of students who play neither?
Answer 25.
Total number of students = 60 ⇒ n(U) = 60
Number of students who play cricket = 25 ⇒ n(C) = 25
Number of students who play tennis = 20 ⇒ n(T) = 20
Number of students who play both the games = 10 ⇒ n(C ∩ T) = 10
∴ n(C ∪ T) = n(C) + n(T) − n(C ∩ T)
= 25 + 20 − 10 = 35
Number of students who play neither
= n(U) − n(C ∪ T)
= 60 − 35 = 25
Question 26. In a survey of 200 students of a school, it was found that 120 study Mathematics, 90 study Physics and 70 study Chemistry, 40 study Mathematics and Physics, 30 study Physics and Chemistry, 50 study Chemistry and Mathematics and 20 none of these subjects. Find the number of students who study all the three subjects
Answer 26.
Total number of students = 200 ⇒ n(U) = 200
Number of students who study Mathematics = 120 ⇒ n(M) = 120
Number of students who study Physics = 90 ⇒ n(P) = 90
Number of students who study Chemistry = 70 ⇒ n(C) = 70
Number of students who study Mathematics and Physics = 40 ⇒ n(M ∩ P) = 40
Number of students who study Physics and Chemistry = 30 ⇒ n(P ∩ C) = 30
Number of students who study Chemistry and Mathematics = 50 ⇒ n(C ∩ M) = 50
Number of students who study none of the subjects = 20
⇒ n(M′ ∩ P′ ∩ C′) = 20
∴
n(U) − n(M′ ∩ P′ ∩ C′) = n(M ∪ P ∪ C)
= 200 − 20 = 180
Now,
n(M ∪ P ∪ C) = n(M) + n(P) + n(C) − n(M ∩ P) − n(P ∩ C) − n(C ∩ M) + n(M ∩ P ∩ C)
= 120 + 90 + 70 − 40 − 30 − 50 + n(M ∩ P ∩ C)
= 180 − 160 + n(M ∩ P ∩ C)
= n(M ∩ P ∩ C)
⇒ n(M ∩ P ∩ C) = 20
Hence, the number of students who study all the three subjects = 20.
Question 27. In a town of 10,000 families it was found that 40% families buy newspaper A, 20% families buy newspaper B, 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers. Find
(a) The number of families which buy newspaper A only.
(b) The number of families which buy none of A, B and C
Answer 27.
In a town of 10,000 families it was found that:
- 40% families buy newspaper A
- 20% families buy newspaper B
- 10% families buy newspaper C
- 5% families buy A and B
- 3% families buy B and C
- 4% families buy A and C
- 2% families buy all the three newspapers
We are to find:
(a) The number of families which buy newspaper A only
We use the formula:
A only = A − (A ∩ B) − (A ∩ C) + (A ∩ B ∩ C)
= 40% − 5% − 4% + 2% = 33%
Number of families = 33% of 10,000 = 3,300
b) The number of families which buy none of A, B and C
We use the principle of inclusion-exclusion to find the number of families that buy at least one of the newspapers A, B, or C:
n(A ∪ B ∪ C)
= n(A) + n(B) + n(C) − n(A ∩ B) − n(B ∩ C) − n(A ∩ C) + n(A ∩ B ∩ C)
Substituting the given percentages:
= 40% + 20% + 10% − 5% − 3% − 4% + 2%
= 60%
So, families that buy at least one newspaper = 60% of 10,000 = 6,000
Therefore, the number of families that buy none of A, B, or C =
10,000 − 6,000 = 4,000
Question 28. If A and B are subsets of the universal set U, then show that
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows:
French = 17, English = 13, Sanskrit = 15
French and English = 09, English and Sanskrit = 4
French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of
students who study
(i) French only (v) French and Sanskrit but not English
(ii) English only (vi) French and English but not Sanskrit
(iii) Sanskrit only (vii) at least one of the three languages
(iv) English and Sanskrit (viii) none of the three languages
but not French
Answer 28.
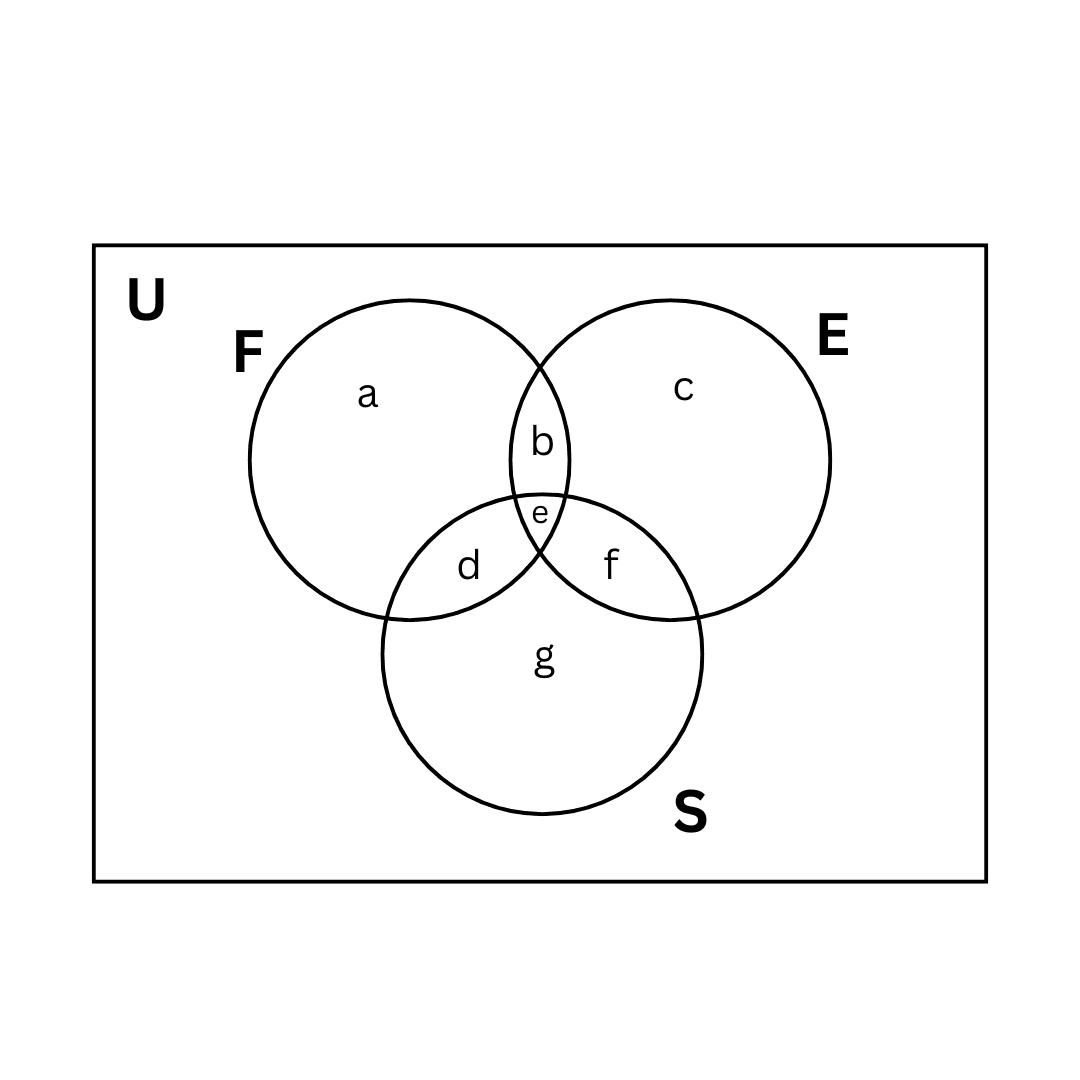
Solution using Venn diagram method:
Total number of students = 50 ⇒ n(U) = 50
Number of students who study French = 17 ⇒ n(F) = 17
Number of students who study English = 13 ⇒ n(E) = 13
Number of students who study Sanskrit = 15 ⇒ n(S) = 15
Number of students who study French and English = 9 ⇒ n(F ∩ E) = 9
Number of students who study English and Sanskrit = 4 ⇒ n(E ∩ S) = 4
Number of students who study French and Sanskrit = 5 ⇒ n(F ∩ S) = 5
Number of students who study French, English and Sanskrit = 3 ⇒ n(F ∩ E ∩ S) = 3
Let the regions in the Venn diagram be represented by:
- a = French only
- b = French and English but not Sanskrit
- c = English only
- d = French and Sanskrit but not English
- e = English and Sanskrit but not French
- f = All three (French, English, Sanskrit)
- g = Sanskrit only
We have the following equations:
- n(F) = a + b + d + e + f = 17 …(i)
- n(E) = b + c + e + f = 13 …(ii)
- n(S) = d + e + f + g = 15 …(iii)
- n(F ∩ E) = b + e + f = 9 …(iv)
- n(E ∩ S) = e + f = 4 …(v)
- n(F ∩ S) = d + f = 5 …(vi)
- n(F ∩ E ∩ S) = f = 3 …(vii)
Now solving:
From (iv): b + e + 3 = 9 ⇒ b + e = 6
From (v): e + 3 = 4 ⇒ e = 1
Then b = 6 − 1 = 5
From (vi): d + 3 = 5 ⇒ d = 2
From (i): a + 5 + 2 + 1 + 3 = 11 ⇒ a = 17 − 11 = 6
From (ii): 5 + c + 1 + 3 = 9 ⇒ c = 13 − 9 = 4
From (iii): 2 + 1 + 3 + g = 6 ⇒ g = 15 − 6 = 9
Final Answers:
(i) Number of students who study French only, a = 6
(ii) Number of students who study English only, c = 3
(iii) Number of students who study Sanskrit only, g = 9
(iv) Number of students who study English and Sanskrit but not French, e = 1
(v) Number of students who study French and Sanskrit but not English, d = 2
(vi) Number of students who study French and English but not Sanskrit, b = 6
(vii) Number of students who study at least one of the three languages:
= a + b + c + d + e + f + g
= 6 + 6 + 3 + 2 + 1 + 3 + 9 = 30
(viii) Number of students who study none of the three languages:
= 50 − 30 = 20