Written by : Anmol Gupta
7 mins read time
NCERT Class 11 Maths Chapter 1 Sets Exercise 1.4 Solutions
Table of Contents
Solved Examples of Exercise 1.4
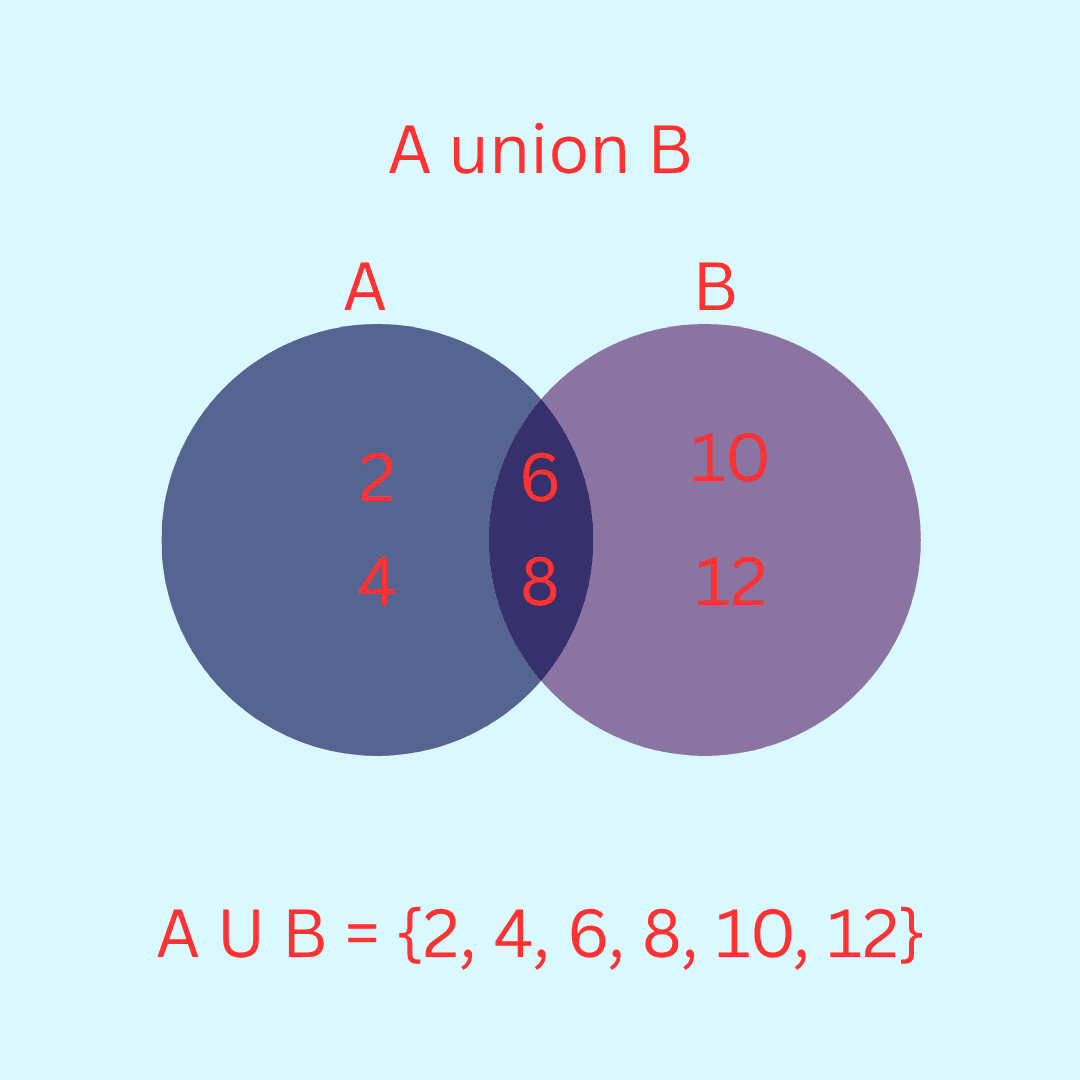
Example 12. Let A = {2, 4, 6, 8} and B = {6, 8, 10, 12}. Find A ∪ B
Answer 12. A ∪ B = { 2, 4, 6, 8, 10, 12}. Note that the common elements 6 and 8 have been taken only once while writing A ∪ B
Example 13. Let A = { a, e, i, o, u } and B = { a, i, u }. Show that A ∪ B = A
Answer 13. A ∪ B = { a, e, i, o, u } = A
If B ⊂ A, then A ∪ B = A

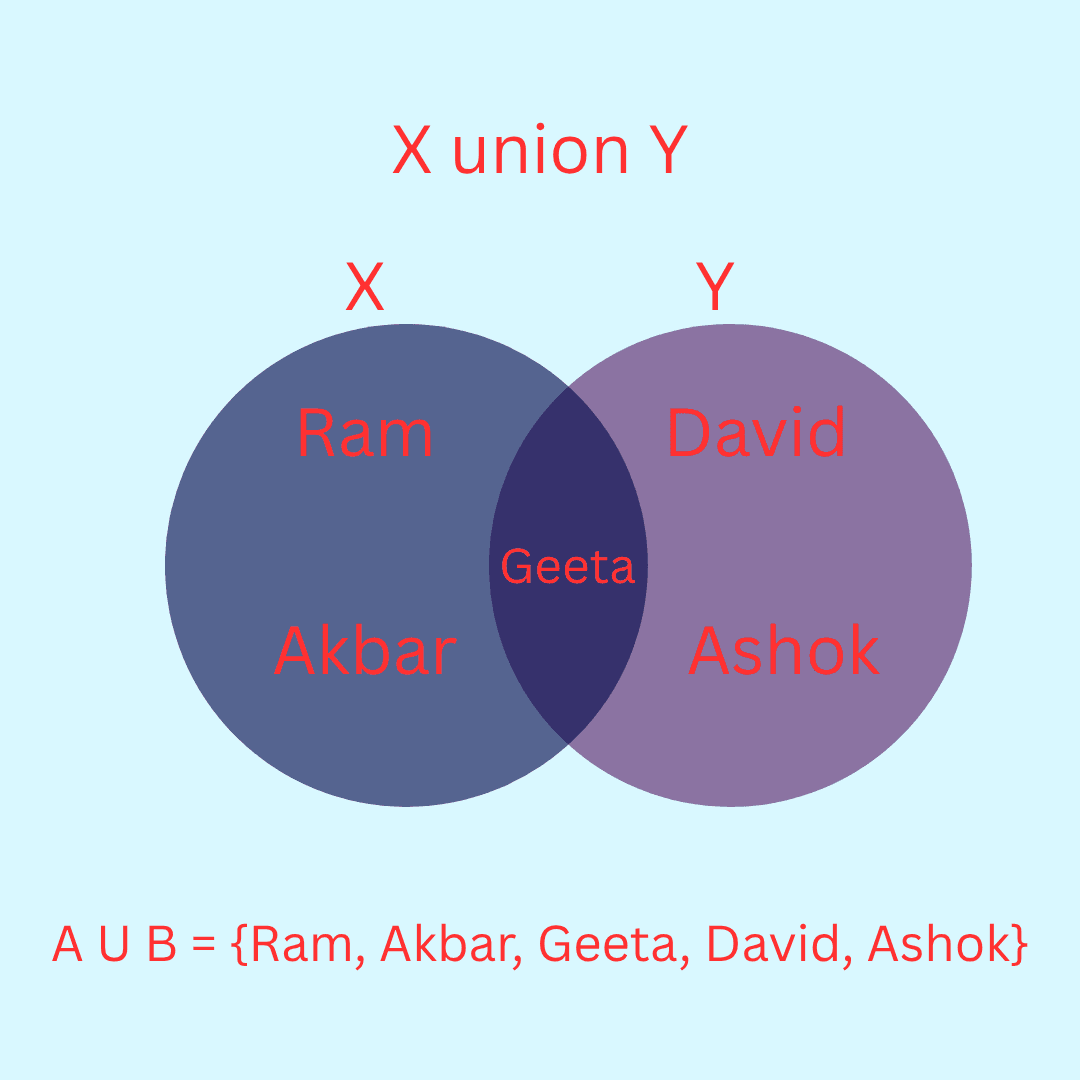
Example 14. Let X = {Ram, Geeta, Akbar} be the set of students of Class XI, who are in school hockey team. Let Y = {Geeta, David, Ashok} be the set of students from Class XI who are in the school football team. Find X ∪ Y and interpret the set.
Answer 14. X ∪ Y = {Ram, Geeta, Akbar, David, Ashok}. This is the set of students from Class XI who are in the hockey team or the football team or both.
Example 15. Consider the sets A and B of Example 12. Find A ∩ B
Answer 15. A = {2, 4, 6, 8} and B = {6, 8, 10, 12}
A ∩ B = {6,8}
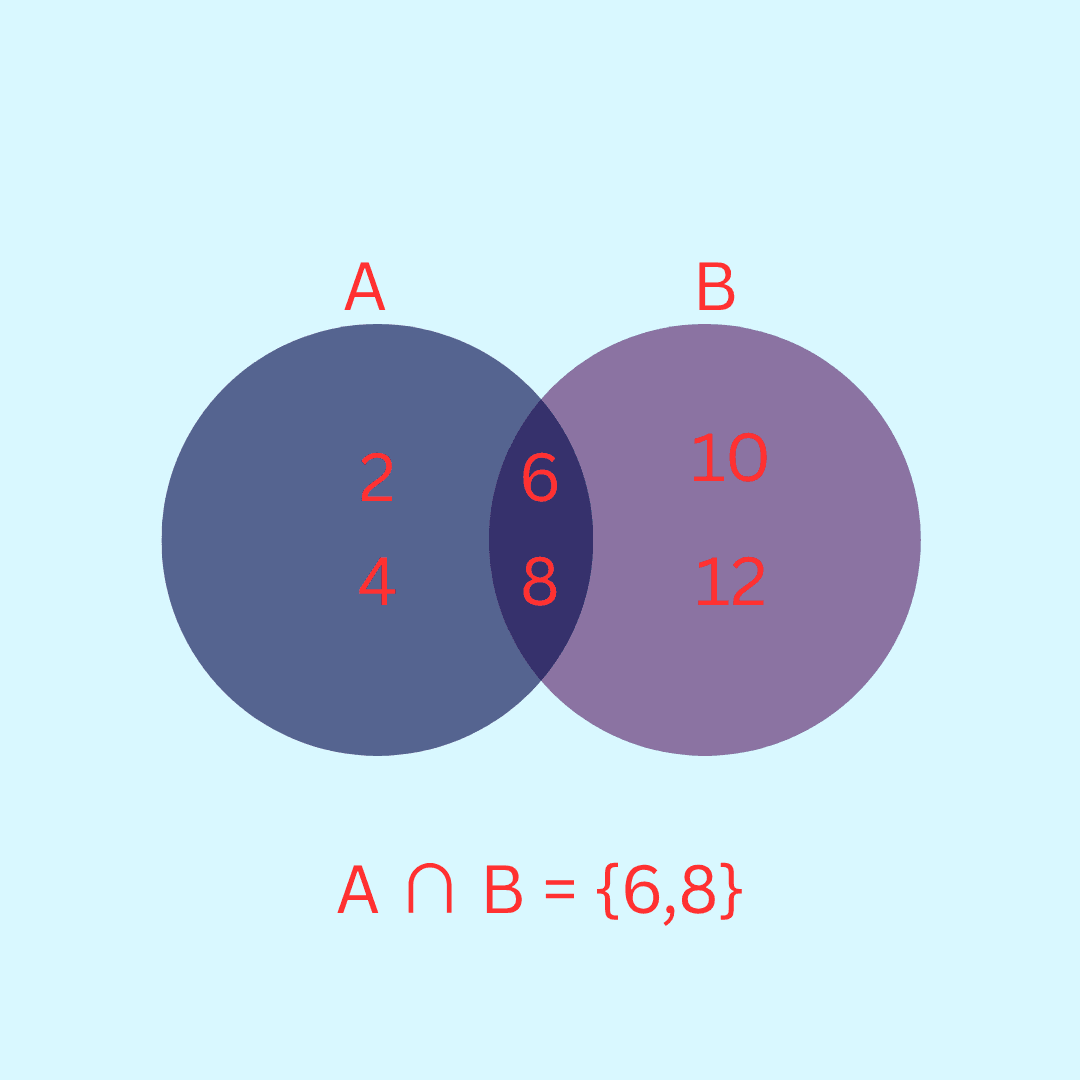
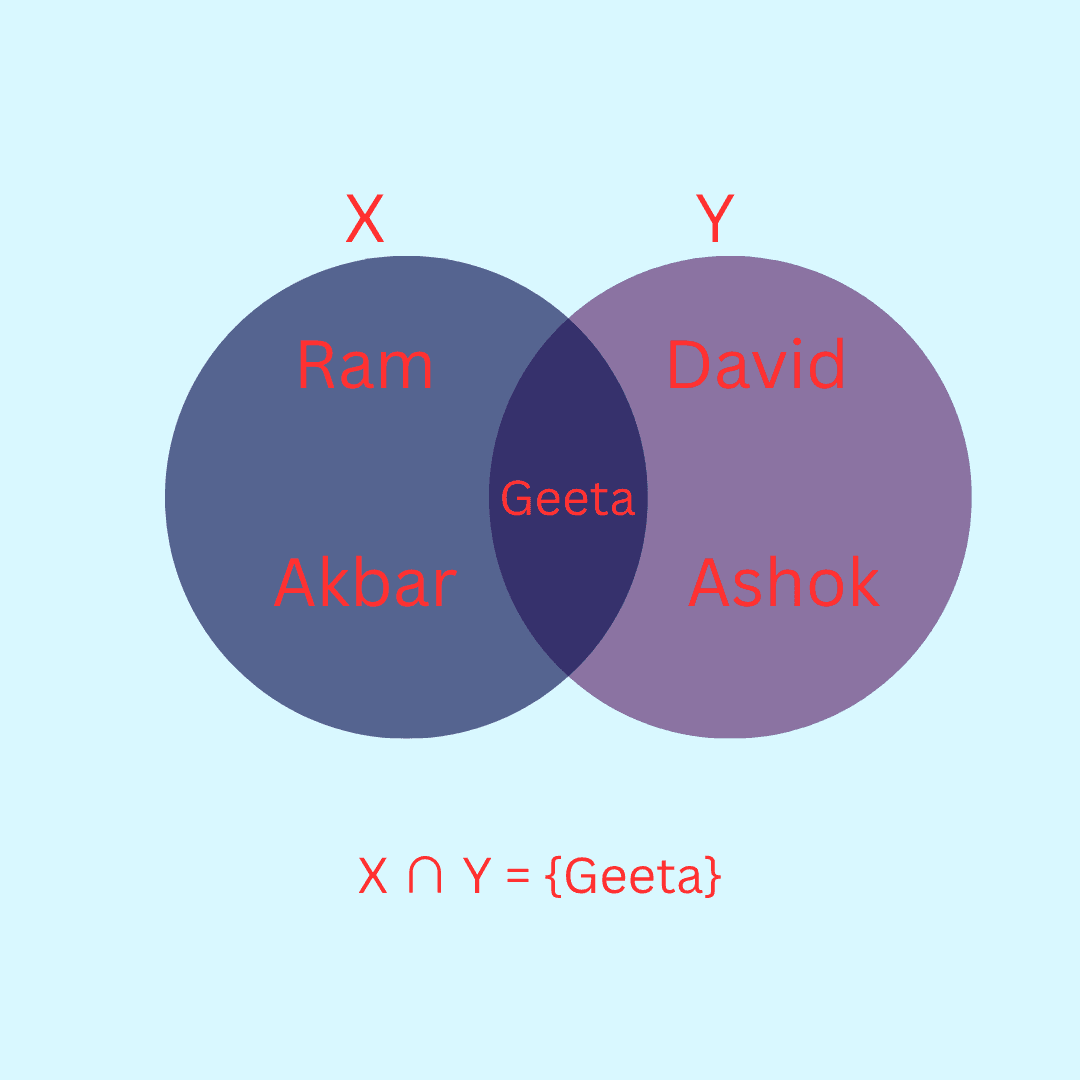
Example 16. Consider the sets X and Y of Example 14. Find X ∩ Y.
Answer 16. X = {Ram, Geeta, Akbar}
Y = {Geeta, David, Ashok}
X ∩ Y = {Geeta}
Example 17. Let A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and B = { 2, 3, 5, 7 }. Find A ∩ B and hence show that A ∩ B = B
Answer 17. A ∩ B = { 2, 3, 5, 7 } = B
B ⊂ A and that A ∩ B = B

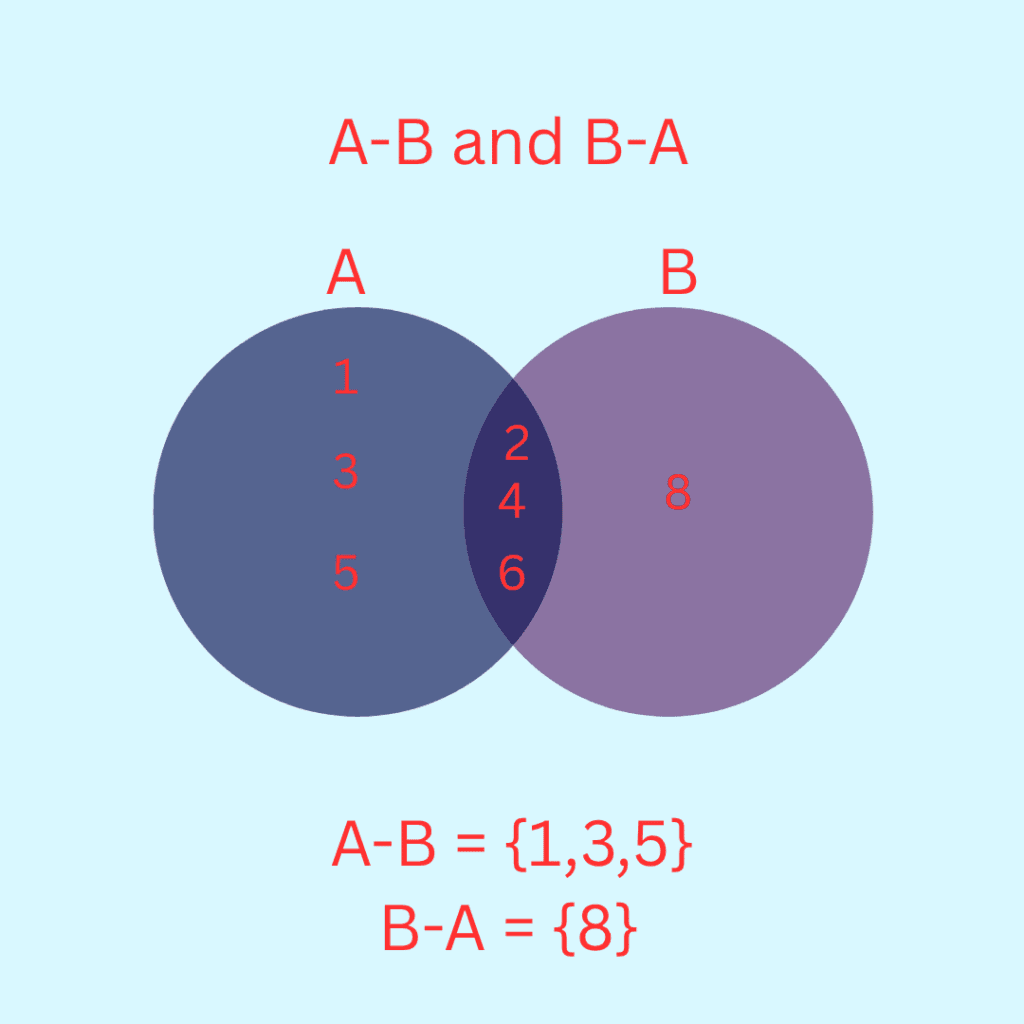
Example 18. Let A = { 1, 2, 3, 4, 5, 6}, B = { 2, 4, 6, 8 }. Find A – B and B – A.
Answer 18. A – B = {1, 3, 5}
B – A = {8}
Example 19. Let V = {a, e, i, o, u} and B = {a, i, k, u}. Find V – B and B – V
Answer 19. V – B = {e, o}
B – V = {k}
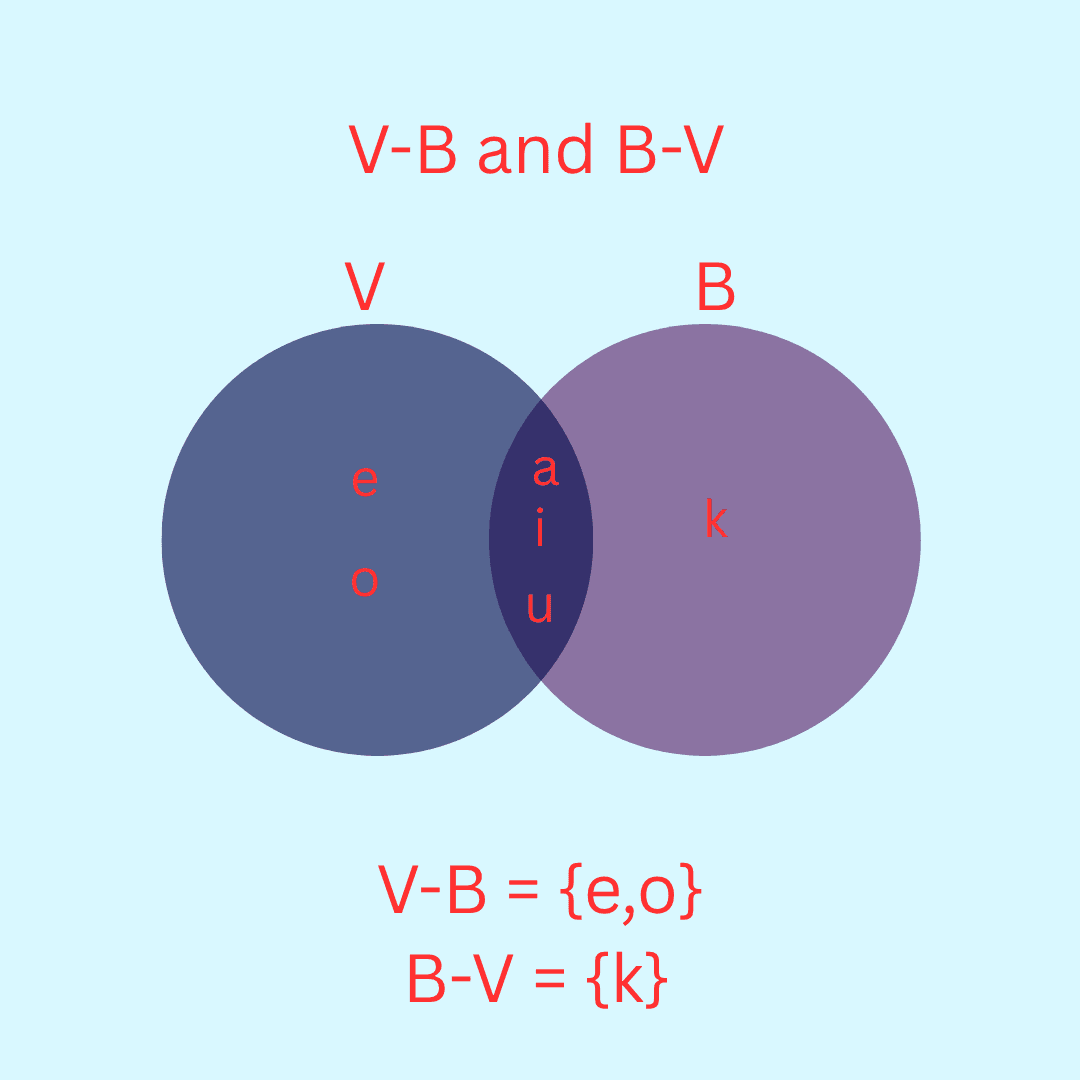
Exercise 1.4 solved questions
Question 1. Find the union of each of the following pairs of sets :
(i) X = {1, 3, 5} Y = {1, 2, 3}
(ii) A = {a, e, i, o, u} B = {a, b, c}
(iii) A = {x : x is a natural number and multiple of 3}
B = {x : x is a natural number less than 6}
(iv) A = {x : x is a natural number and 1 < x ≤6 }
B = {x : x is a natural number and 6 < x < 10 }
(v) A = {1, 2, 3}, B = φ
Answer 1.
(i) X ∪ Y = {1,2,3,5}
(ii) A ∪ B = {a, b, c, e, i, o, u}
(iii) A = {3,6,9,…}
B = {1,2,3,4,5}
A ∪ B = {1,2,3,4,5,6,9,12…}
(iv) A = {2,3,4,5,6}
B = {7,8,9}
A ∪ B = {2,3,4,5,6,7,8,9}
(v) A ∪ B = {1,2,3} = A
Question 2. Let A = { a, b }, B = {a, b, c}. Is A ⊂ B ? What is A ∪ B ?
Answer 2.
Yes A ⊂ B as every element of A is in B
A ∪ B = {a, b, c} = B
Question 3. If A and B are two sets such that A ⊂ B, then what is A ∪ B ?
Answer 3.
Let a ∈ A
Let a, b, c ∈ B
Here including element ‘a’ in set B is important as it is given that A ⊂ B
A ∪ B = {a, b, c} = B
Question 4. If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8 } and D = { 7, 8, 9, 10 }; find
(i) A ∪ B (ii) A ∪ C (iii) B ∪ C (iv) B ∪ D
(v) A ∪ B ∪ C (vi) A ∪ B ∪ D (vii) B ∪ C ∪ D
Answer 4.
(i) A ∪ B = {1,2,3,4,5,6}
(ii) A ∪ C = {1,2,3,4,5,6,7,8}
(iii) B ∪ C = {3,4,5,6,7,8}
(iv) B ∪ D = {3,4,5,6,7,8,9,10}
(v) A ∪ B ∪ C = {1,2,3,4,5,6,7,8}
(vi) A ∪ B ∪ D = {1,2,3,4,5,6,7,8,9,10}
(vii) B ∪ C ∪ D = {3,4,5,6,7,8,9,10}
Question 5. Find the intersection of each pair of sets of question 1 above.
Answer 5.
(i) X ∩ Y = {1,3}
(ii) A ∩ B = {a}
(iii)A ∩ B = {3}
(iv) A ∩ B = {ɸ}
(v) Given:
A = {1, 2, 3}
B = ∅ (the empty set)
Intersection of A and B:
The intersection of two sets A ∩ B is the set of elements that are common to both A and B.
Since B is an empty set, it has no elements, so there can’t be any elements common to both.
Therefore:
A ∩ B = ∅
Answer: The intersection of A and B is the empty set.
Question 6. If A = { 3, 5, 7, 9, 11 }, B = {7, 9, 11, 13}, C = {11, 13, 15} and D = {15, 17}; find
(i) A ∩ B (ii) B ∩ C (iii) A ∩ C ∩ D
(iv) A ∩ C (v) B ∩ D (vi) A ∩ (B ∪ C)
(vii) A ∩ D (viii) A ∩ (B ∪ D) (ix) ( A ∩ B ) ∩ ( B ∪ C )
(x) ( A ∪ D) ∩ ( B ∪ C)
Answer 6. (i) A ∩ B = {7,9,11}
(ii) B ∩ C = {11,13}
(iii) A ∩ C ∩ D = ɸ
(iv) A ∩ C = {11}
(v) B ∩ D = ɸ
(vi) A ∩ (B ∪ C) = A ∩ {7,9,11,13,15} = {7,9,11}
(vii) A ∩ D = ɸ
(viii) A ∩ (B ∪ D) = A ∩ {7,9,11,13,15,17} = {7,9,11}
(ix) ( A ∩ B ) ∩ ( B ∪ C ) = {7,9,11} ∩ {7,9,11,13,15} = {7,9,11}
(x) ( A ∪ D) ∩ ( B ∪ C) = { 3,5,7,9,11,15,17 } ∩ {7,9,11,13,15} = {7,9,11,15}
Question 7. If A = {x : x is a natural number }, B = {x : x is an even natural number} C = {x : x is an odd natural number} and D = {x : x is a prime number }, find
(i) A ∩ B (ii) A ∩ C (iii) A ∩ D
(iv) B ∩ C (v) B ∩ D (vi) C ∩ D
Answer 7.
A = {1,2,3,4,5,6…}
B = {2,4,6,8..}
C = {1,3,5,7…}
D = {2,3,5,7,11,13…}
(i) A ∩ B = B as B ⊂ A, every even natural number is a natural number
(ii) A ∩ C = C as C ⊂ A, every even natural number is a natural number
(iii) A ∩ D = D as D ⊂ A, every even natural number is a natural number
(iv) B ∩ C = ɸ as there is no natural number which is both even and odd
(v) B ∩ D = {2} as 2 is only even prime number
(vi) C ∩ D = { x : x is an odd prime number }
Question 8. Which of the following pairs of sets are disjoint
(i) {1, 2, 3, 4} and {x : x is a natural number and 4 ≤ x ≤ 6 }
(ii) { a, e, i, o, u } and { c, d, e, f }
(iii) {x : x is an even integer } and {x : x is an odd integer}
Answer 8.
(i) Not disjoint as 4 is common to both sets given
(ii) Not disjoint as element e is common to both sets given
(iii) Given sets are disjoint as there is no natural number that is both even and odd
Question 9. If A = {3, 6, 9, 12, 15, 18, 21}, B = { 4, 8, 12, 16, 20 },
C = { 2, 4, 6, 8, 10, 12, 14, 16 }, D = {5, 10, 15, 20 }; find
(i) A – B (ii) A – C (iii) A – D (iv) B – A
(v) C – A (vi) D – A (vii) B – C (viii) B – D
(ix) C – B (x) D – B (xi) C – D (xii) D – C
Answer 9.
(i) A-B = {3,6,9,15,18,21}
(ii) A-C = {3,9,15,18,21}
(iii) A-D = {3,6,9,12,18,21}
(iv) B-A = {4,8,16,20}
(v) C-A = { 2, 4, 8, 10, 14, 16 }
(vi) D-A = {5,10,20}
(vii) B-C = {20}
(viii) B-D = {4,8,12,16}
(ix) C-B = {2,6,10,14}
(x) D-B ={5,10,15}
(xi) C-D = { 2, 4, 6, 8, 12, 14, 16 }
(xii) D-C = {5,15,20}
Question 10. If X= { a, b, c, d } and Y = {f, b, d, g}, find
(i) X – Y (ii) Y – X (iii) X ∩ Y
Answer 10.
(i) X-Y = {a,c}
(ii) Y-X = {f,g}
(iii) X ∩ Y = {b,d}
Question 11. If R is the set of real numbers and Q is the set of rational numbers, then what is R – Q?
Answer 11. R-Q is the set of irrational numbers
Question 12. State whether each of the following statement is true or false. Justify your answer.
(i) { 2, 3, 4, 5 } and {3, 6} are disjoint sets.
(ii) { a, e, i, o, u } and { a, b, c, d } are disjoint sets.
(iii) { 2, 6, 10, 14 } and {3, 7, 11, 15} are disjoint sets.
(iv) { 2, 6, 10 } and {3, 7, 11} are disjoint sets
Answer 12.
(i) False as element 3 is common to both the sets
(ii) False as element a is common to both the sets
(iii) True as no element is common to both the sets
(iv) True as no element is common to both the sets

