Understand concepts involved in topic ratios
Last updated : 29 June 2024, Saturday
Verified for accuracy
Ratio

Ratios are fundamental mathematical expressions used to compare and relate quantities in various contexts. They are used to establish proportional relationships, make comparisons, and analyze the relative sizes of different quantities. Ratios are expressed as a fraction, often written as “a:b” or “a to b,” where “a” and “b” represent two different quantities or values. These values could be numbers, measurements, or any data points that can be quantified.
Here are some key aspects of ratios:
- Comparing Quantities: Ratios are primarily used to compare the size or magnitude of one quantity in relation to another. For example, if you want to compare the number of boys to girls in a classroom, you might express the ratio as “5:3,” meaning there are 5 boys for every 3 girls.
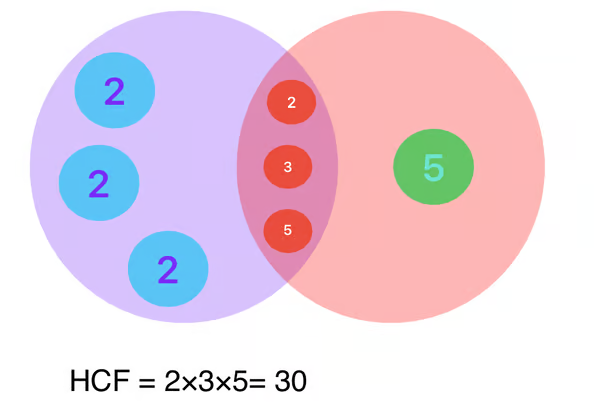
- Simplification: Ratios can be simplified by dividing both terms by their greatest common factor. For example, if you have a ratio of 6:8, you can simplify it to 3:4 by dividing both numbers by 2.
- Proportions: Ratios can be used to create proportions. A proportion is an equation that states two ratios are equal. For example, if you have the ratios 2:3 and 4:6, you can set up the proportion (2/3) = (4/6).
- Scaling: Ratios can be used to scale up or down quantities. If you have a recipe that serves 4 people but you want to serve 8, you can use the ratio of 4:8 to adjust the quantities of ingredients.
- Percentages: Ratios are often used to express percentages. For example, a ratio of 3:5 can be converted to a percentage by dividing the first number (3) by the sum of both numbers (3 + 5), which equals 0.375 or 37.5%.
- Financial Analysis: In finance, ratios are essential for evaluating a company’s financial health and performance. Common financial ratios include the debt-to-equity ratio, price-to-earnings ratio, and current ratio, among others.