Logarithms | unipolaris academy

Understand concepts involved in topic logarithms

Last updated : 29 June 2024, Saturday

Verified for accuracy

Introduction

Logarithms are a fundamental concept in mathematics, particularly useful in various fields such as algebra, calculus, and complex number theory. They are the inverse operation of exponentiation, just as division is the inverse of multiplication.

Definition of Logarithms

The logarithm of a number is the exponent to which another fixed number, the base, must be raised to produce that number.

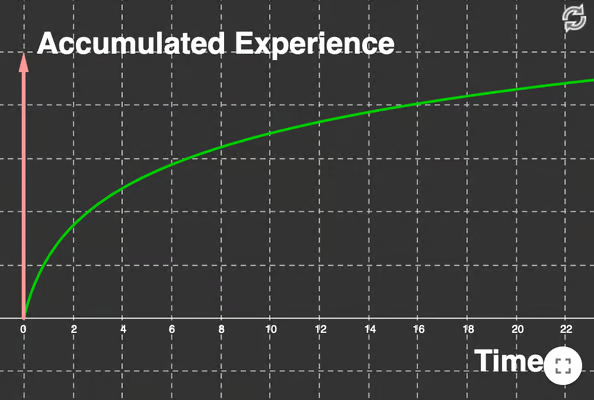
Explore logarithm graph

CLICK TO EXPLORE TOOL

Types of Logarithms

Properties of Logarithms

Derivations of important formulas

Fractions come in different forms, and understanding these types is crucial in working with them effectively:

Questions and Answers

Applications of Logarithms

1. Solving Exponential Equations: Logarithms can be used to solve equations where the variable is an exponent.

2. Complex Calculations: They simplify multiplication into addition and powers into multiplication, which makes complex calculations easier.

3. Scientific Applications: In fields like chemistry, biology, astronomy, and geology, logarithms help in dealing with large quantities and exponential growth or decay.

4. Sound and Earthquake Measurement: The decibel scale for sound and the Richter scale for earthquake magnitude are logarithmic scales

5. Computer Science: Logarithms are used in algorithms, complexity analysis, and data structures like binary trees.

6. Finance: Logarithms are used in calculating compound interest and in other financial formulas.

Quiz

Logarithms

Questions 1-10 have single answer correct

Questions 11-20 can have one or more than one single answer correct

1 / 20

If log(x) + log(5) = 1, what is the value of x?

2 / 20

What is the base b if log_b64 = 3?

3 / 20

What is the value of log₂64?

4 / 20

If logₓ100 = 2, what is the value of x?

100

5 / 20

Which of the following is equivalent to log₁₀(x²y)

2log₁₀x + log₁₀y

log₁₀x + log₁₀y

log₁₀x² + y

2(log₁₀x + log₁₀y)

6 / 20

If log_b3 = 0.5 and log_b2 = 0.3, what is log_b12?

1.1

0.8

0.9

1.0

7 / 20

What is the solution of 10²ˣ = 1000?

1.5

2.5

8 / 20

Which of the following is the inverse function of y = log₁₀x?

y = 10ˣ

y = eˣ

y = x¹⁰

y = ln x

9 / 20

If log5 = a and log2 = b, what is log10 0.4 in terms of a and b?

-a + b

a – b

b – a

-2a + b

10 / 20

What is the value of log₃81?

11 / 20

The value of log₁₀100 is:

12 / 20

If log_ba = 2 and logₐb = 1⁄2, then a and b are:

Reciprocals of each other

Equal

Squares of each other

One is the square root of the other

13 / 20

The expression log₁₀(10ˣ) simplifies to:

10ˣ

xlog₁₀10

14 / 20

If logₐx = y, then x is equal to:

aʸ

10⁹

yᵃ

1/a⁹

15 / 20

Which of the following is/are true for logarithms?

log_b (MN) = log_bM + log_bN

log_b M/N= log_bM – log_bN

log_b(Mᵏ) = k log_bM

log_bM =logₐM /logₐb

16 / 20

If log₂x =3 and log₂y = 4, then log₂(xy) is:

17 / 20

The base of the logarithm in the equation log x = 10

Implied to be 10

18 / 20

For x > 0, logₓ1 is always:

Undefined

19 / 20

If logₐb – cc, then logₐ² b² is:

C/2

c²

1/c

20 / 20

The inverse of the function f(x) = log_bx is:

bˣ

logₓb

1/log_bx

Your score is

The average score is 0%

Conclusion

Logarithms are not just a mathematical tool but a concept that offers a new perspective on understanding growth, decay, and the nature of exponential change. Their versatility and application in various scientific and practical domains make them an indispensable part of the mathematical toolkit.

< Exponents and powers

Solving linear Equations >