Last Updated:
Written by:
Time to read:
NCERT Exemplar Class 11 Maths Chapter 2 Relations and Functions Examples Solutions
Table of Contents
Solved Examples
Short Answer Type
Example 1 Let A = {1, 2, 3, 4} and B = {5, 7, 9}. Determine
(i) A × B
(ii) B × A
(iii) Is A × B = B × A ?
(iv) Is n (A × B) = n (B × A) ?
Answer 1 Since A = {1, 2, 3, 4} and B = {5, 7, 9}. Therefore,
(i) A × B = {(1, 5), (1, 7), (1, 9), (2, 5), (2, 7), (2, 9), (3, 5), (3, 7), (3, 9), (4, 5), (4, 7), (4, 9)}
(ii) B × A = {(5, 1), (5, 2), (5, 3), (5, 4), (7, 1), (7, 2), (7, 3), (7, 4), (9, 1), (9, 2), (9, 3), (9, 4)}
(iii) No, A × B ≠ B × A. Since A × B and B × A do not have exactly the same ordered pairs.
(iv) n (A × B) = n (A) × n (B) = 4 × 3 = 12
n (B × A) = n (B) × n (A) = 4 × 3 = 12
Hence n (A × B) = n (B × A)
Example 2 Find x and y if:
(i) (4x + 3, y) = (3x + 5, – 2) (ii) (x – y, x + y) = (6, 10)
Answer 2. (i) Since (4x + 3, y) = (3x + 5, – 2), so
4x + 3 = 3x + 5
or x = 2
and y = – 2
(ii) x – y = 6
x + y = 10
∴ 2x = 16
or x = 8
8 – y = 6
∴ y = 2
Example 3. If A = {2, 4, 6, 9} and B = {4, 6, 18, 27, 54}, a ∈ A, b ∈ B, find the set of ordered pairs such that ‘a’ is factor of ‘b’ and a < b
Answer 3. Since A = {2, 4, 6, 9}
B = {4, 6, 18, 27, 54},
we have to find a set of ordered pairs (a, b) such that a is factor of b and a < b.
Since 2 is a factor of 4 and 2 < 4.
So (2, 4) is one such ordered pair.
Similarly, (2, 6), (2, 18), (2, 54) are other such ordered pairs. Thus the required set of ordered pairs is
{(2, 4), (2, 6), (2, 18), (2, 54), (6, 18), (6, 54,), (9, 18), (9, 27), (9, 54)}
Example 4. Find the domain and range of the relation R given by
R = {(x, y) : y = x + ⁶⁄ₓ ; where x, y ∈ N and x < 6}.
Answer 4. When x = 1, y = 7 ∈ N, so (1, 7) ∈ R. Again for,
x = 2 . y = 2 + ⁶⁄₂ = 2 + 3 = 5 ∈ N, so (2, 5) ∈ R. Again for
x = 3, y = 3 + ⁶⁄₃ = 3 + 2 = 5 ∈ N, (3, 5) ∈ R. Similarly for x = 4
y = 4 + ⁶⁄₄ ∉ N and for x = 5 , y = 5 + ⁶⁄₅ ∉ N
Thus R = {(1, 7), (2, 5), (3, 5)}, where Domain of R = {1, 2, 3}
Range of R = {7, 5}
Example 5. Is the following relation a function? Justify your answer
(i) R1= {(2, 3), (1/2,0), (2,7), (-4,6)}
(ii) R2 = {(x, |x|) | x is a real number}
Answer 5. (i) Since (2, 3) and (2, 7) ∈ R1
⇒R1(2) = 3 and R1(2) = 7
So R1(2) does not have a unique image. Thus R1 is not a function
(ii) R2 = {(x, |x|) | x ∈R}
For every x ∈ R there will be unique image as |x| ∈ R.
Therefore R2 is a function.
Example 6. Find the domain for which the functions
f(x) = 2x2 – 1 and g (x) = 1 – 3x are equal.
Answer 6.
For f (x) = g (x)
⇒ 2x2 – 1 = 1 – 3x
⇒ 2x2 + 3x – 2 = 0
⇒2x2 + 4x – x – 2 = 0
⇒ 2x (x + 2) – 1 (x + 2) = 0
⇒ (2x – 1) (x + 2) = 0
Thus domain for which the function f (x) = g (x) is { 1/2, -2 }
Example 7. Find the domain of each of the following functions:
(i) f(x) = ˣ⁄ₓ₂ ₊ ₃ₓ ₊ ₂
(ii) f(x) = [x] + x
Answer 7. (i) f is a rational function of the form g(x)/h(x) where, g (x) = x and h (x) = x2 + 3x + 2
Now h (x) ≠ 0 ⇒ x2 + 3x + 2 ≠ 0 ⇒ (x + 1) (x + 2) ≠ 0 and hence domain of the given function is R – {– 1, – 2}
(ii)f (x) = [x] + x,i.e., f (x) = h (x) + g (x)
where h (x) = [x] and g (x) = x
The domain of h = R
and the domain of g = R. Therefore Domain of f = R
Example 8. Find the range of the following functions given by
(i)
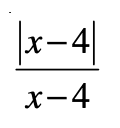
(ii) √(16 − x²)
Answer 8.
(i) f(x) = |x − 4| / (x − 4)
= (x − 4)/(x − 4) = 1, x > 4
= −(x − 4)/(x − 4) = −1, x < 4
Thus, the range of |x − 4| / (x − 4) is {1, −1}.
(ii)
The domain of f, where
f(x) = √(16 − x²),
is [−4, 4].
For the range, let
y = √(16 − x²)
Then
y² = 16 − x²
or
x² = 16 − y²
Since x ∈ [−4, 4],
Thus, the range of f is [0, 4].
Example 9. Redefine the function which is given by
f(x) = |x − 1| + |1 + x|, −2 ≤ x ≤ 2
Answer 9.
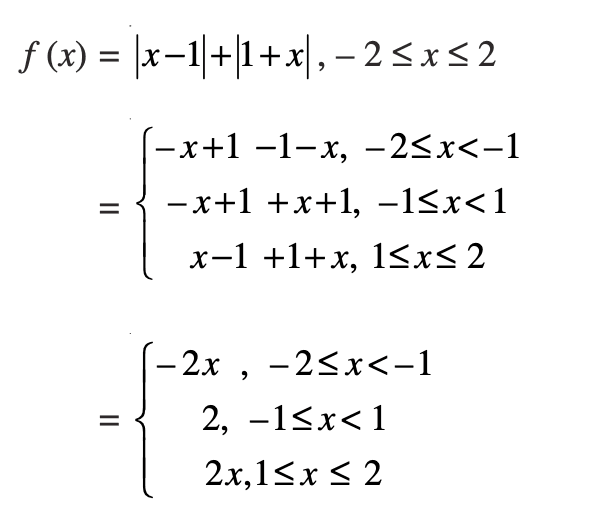
Example 10. Find the domain of the function f given by
f (x) = 1 / √( [x]² − [x] − 6 )
Answer 10.
Given that
f(x) = 1 / √( [x]² − [x] − 6 ),
f is defined if
[x]² − [x] − 6 > 0
or
([x] − 3)([x] + 2) > 0
⇒ [x] < −2 or [x] > 3
⇒ x < −2 or x ≥ 4
Hence,
Domain = (−∞, −2) ∪ [4, ∞).
Objective Type Questions
Choose the correct answer out of the four given possible answers (M.C.Q.)
Example 11. The domain of the function f defined by
f (x) = 1 / √( x − |x| ) is
(A) R
(B) R+
(C) R–
(D) None of these
Answer 11. The correct answer is (D).
Given that
f(x) = 1 / √(x − |x|)
where
x − |x| =
• x − x = 0, if x ≥ 0
• 2x, if x < 0
Thus,
For x ≥ 0:
x − |x| = 0
⇒ √(x − |x|) = 0
⇒ f(x) is not defined.
For x < 0:
x − |x| = 2x < 0
⇒ √(x − |x|) is not real
⇒ f(x) is not defined.
Hence,
1 / √(x − |x|) is not defined for any x ∈ R.
Therefore,
f is not defined for any x ∈ R,
i.e. Domain of f is none of the given options.
Example 12.
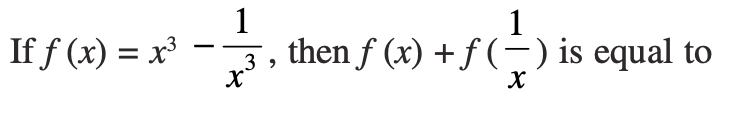

Answer 12. The correct choice is C.
Since
f(x) = x³ − 1/x³
f(1/x) = 1/x³ − x³
Hence,
f(x) + f(1/x)
= x³ − 1/x³ + 1/x³ − x³
= 0
Example 13. Let A and B be any two sets such that n(B) = p, n(A) = q then the total number of functions f : A → B is equal to __.
Answer 13. Any element of set A, say xi can be connected with the element of set B in p ways. Hence, there are exactly pq functions.
Example 14. Let f and g be two functions given by
f = {(2, 4), (5, 6), (8, – 1), (10, – 3)}
g = {(2, 5), (7, 1), (8, 4), (10, 13), (11, – 5)} then. Domain of f + g is __
Answer 14.
Since Domain of f = Df = {2, 5, 8, 10} and
Domain of g = Dg = {2, 7, 8, 10, 11},
therefore the domain of f + g = {x | x ∈ D f ∩ Dg} = {2, 8, 10}
