Last Updated:
Written by:
Time to read:
NCERT Class 11 Maths Chapter 2 Relations and Functions Miscellaneous Exercise Solutions
Table of Contents
Solved Miscellaneous Examples
Example 18 Let R be the set of real numbers.
Define the real function f: R→R by f(x) = x + 10 and sketch the graph of this function.
Answer 18 Here f(0) = 10, f(1) = 11, f(2) = 12, …, f(10) = 20, etc., and f(–1) = 9, f(–2) = 8, …, f(–10) = 0 and so on.
Therefore, shape of the graph of the given function assumes the form as shown in figure
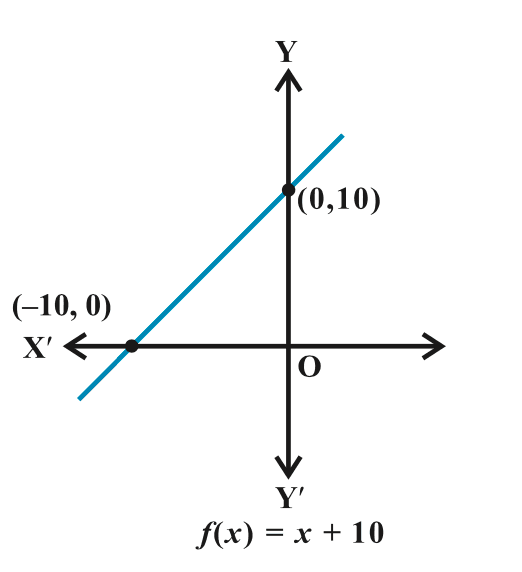
Example 19 Let R be a relation from Q to Q defined by R = {(a,b): a,b ∈ Q and a – b ∈ Z}. Show that
(i) (a,a) ∈ R for all a ∈ Q
(ii) (a,b) ∈ R implies that (b, a) ∈ R
(iii) (a,b) ∈ R and (b,c) ∈ R implies that (a,c)∈R
Answer 19. This problem asks you to prove three specific properties for a relation R defined on the set of rational numbers Q. The condition for two numbers to be related is that their difference must be an integer.
Step-by-step Solution:
(i) Prove that (a,a) ∈ R for all a ∈ Q
This is known as the Reflexive Property.
To check if (a,a) is in the relation, we look at the difference: a-a
- a−a = 0
- Since 0 is an integer ( 0∈Z ), the condition for the relation is satisfied.
Conclusion: (a,a)∈R for all a∈Q.
(ii) Prove that (a,b)∈R implies (b,a)∈R
This is known as the Symmetric Property.
- Assume (a,b)∈R. This means that a−b is an integer. Let a−b = k, where k∈Z.
- To check whether (b,a)∈R, consider the difference: b−a=−(a−b)=−k
- Since k is an integer, its negative (-k) is also an integer, the condition is satisfied.
Conclusion:
Because their difference is an integer, (b,a)∈R.
(iii) Prove that (a,b)∈R and (b,c)∈R implies (a,c)∈R
This is known as the Transitive Property.
- Assume (a,b)∈R and (b,c)∈R.
- This means:
- a−b is an integer, let’s call it k1 and b – c is an integer, let us call it k2
- We need to check if (a, c) is in the relation by looking at a – c.
- We can write a-c as: (a-b) + (b-c)
- Substituting our integers: a-c = k1 + k2
- Since the sum of two integers k1 + k2 is always an integer, the condition is satisfied.
Conclusion : (a,c)∈R.
Final Conclusion
Since the relation R satisfies all three properties:
- Reflexive
- Symmetric
- Transitive
The relation R is an Equivalence Relation.
Example 20 Let f = {(1,1), (2,3), (0, –1), (–1, –3)} be a linear function from Z into Z. Find f(x).
Answer 20 Since f is a linear function, f (x) = mx + c. Also, since (1, 1), (0, – 1) ∈ R, f(1) = m + c = 1 and f (0) = c = –1. This gives m = 2 and f(x) = 2x – 1.
Example 21

Answer 21 Since x2 – 5x + 4 = (x – 4) (x –1), the function f is defined for all real numbers except at x = 4 and x = 1.
Hence the domain of f is R – {1, 4}.
Example 22

Draw the graph of f (x)
Answer 22
Here, f(x) = 1 – x, x < 0, this gives
f(– 4) = 1 – (– 4) = 5
f(– 3) =1 – (– 3) = 4,
f(– 2) = 1 – (– 2) = 3
f(–1) = 1 – (–1) = 2; etc,
and f(1) = 2, f (2) = 3, f (3) = 4
f(4) = 5 and so on for f(x) = x + 1, x > 0.
Thus, the graph of f is as shown in figure
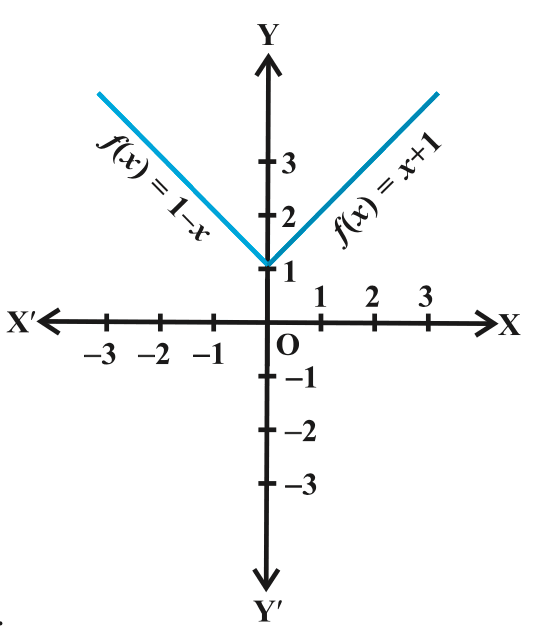
Miscellaneous Exercise on Chapter 2
Question 1.
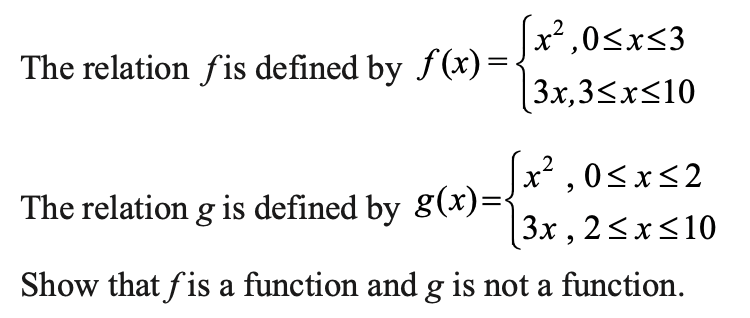
Answer 1.
For a relation to be a function, every input x must have exactly one unique output y.
The domain of f is [0, 10].
For each x ∈ [0, 3), f(x) = x² is uniquely defined, i.e. each x ∈ [0, 3) has a unique image.
For each x ∈ (3, 10], f(x) = 3x is uniquely defined.
At x = 3, x² = 3² = 9. Also, 3x = 3 × 3 = 9, so that f is uniquely defined at 3.
Since every point of the domain has one and only one image under f, this relation is a function.
The domain of g is [0, 10].
For each x ∈ [0, 2), g(x) = x² is uniquely defined.
For each x ∈ (2, 10], g(x) = 3x is uniquely defined.
At x = 2, g(x) = x² = 2² = 4. Also, at x = 2, g(x) = 3x = 3 × 2 = 6.
Now, 2 is in the domain of g and the image of 2 under g is not unique since (2, 4), (2, 6) ∈ g.
Therefore, g is not a function.
Question 2.
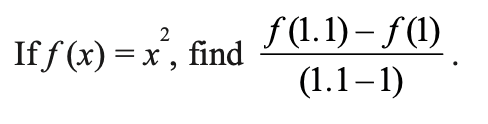
Answer 2.

Question 3.

Answer 3.
Factor the numerator:
x² + 2x + 1 = (x + 1)²
Factor the denominator:
x² − 8x + 12 = (x − 2)(x − 6)
The function is not defined when the denominator is zero.
x − 2 = 0 ⇒ x = 2
x − 6 = 0 ⇒ x = 6
Domain of the function:
All real numbers except 2 and 6.
In interval notation:
(−∞, 2) ∪ (2, 6) ∪ (6, ∞)
Question 4.
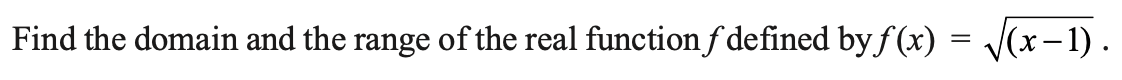
Answer 4.
Given:
f(x) = √(x − 1)
Domain:
For the square root to be defined, the expression inside the root must be greater than or equal to zero.
x − 1 ≥ 0
x ≥ 1
So, the domain is:
[1, ∞)
Range:
The square root of any non-negative number is always non-negative.
√(x − 1) ≥ 0
So, the range is:
[0, ∞)
Final Answer:
Domain: [1, ∞)
Range: [0, ∞)
Question 5. Find the domain and the range of the real function f defined by f(x) = |x-1|
Answer 5.
Given:
f(x) = |x − 1|
Domain:
The absolute value function is defined for all real numbers.
So, the domain is:
(−∞, ∞)
Range:
The absolute value of any real number is always non-negative.
|x − 1| ≥ 0
The minimum value occurs when x − 1 = 0, i.e., x = 1.
Minimum value of f(x) = 0
So, the range is:
[0, ∞)
Final Answer:
Domain: (−∞, ∞)
Range: [0, ∞)
Question 6.

Answer 6. Given:
f = { (x, x² / (1 + x²)) : x ∈ R }
That is,
f(x) = x² / (1 + x²)
Step 1: Let
y = x² / (1 + x²)
Step 2: Rewrite the expression
y(1 + x²) = x²
y + yx² = x²
y = x² − yx²
y = x²(1 − y)
Step 3: Solve for x²
x² = y / (1 − y)
Step 4: Apply conditions
Since x² ≥ 0, we must have:
y / (1 − y) ≥ 0
This is possible only when:
y ≥ 0 and 1 − y > 0
So,
0 ≤ y < 1
Range of the function:
[0, 1)
Question 7.
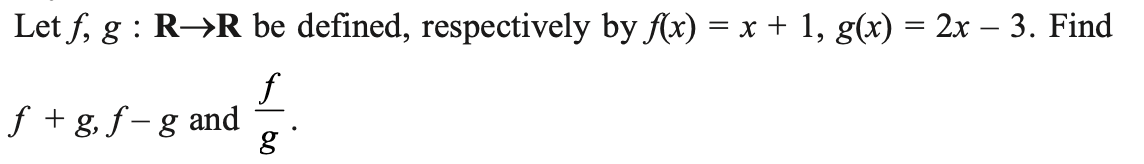
Answer 7.
(f + g)(x) = f(x) + g(x)
= (x + 1) + (2x − 3)
= 3x − 2
(f − g)(x) = f(x) − g(x)
= (x + 1) − (2x − 3)
= −x + 4
(f / g)(x) = f(x) / g(x), g(x) ≠ 0
= (x + 1) / (2x − 3), 2x − 3 ≠ 0
So,
(f / g)(x) = (x + 1) / (2x − 3), x ≠ 3/2
Question 8. Let f = {(1,1), (2,3), (0,–1), (–1, –3)} be a function from Z to Z defined by f(x) = ax + b, for some integers a, b. Determine a, b.
Answer 8.
Given:
f(x) = ax + b …(i)
Now, (1, 1) ∈ f
⇒ f(1) = 1
Replacing x by 1 in (i), we have
f(1) = a × 1 + b
⇒ 1 = a + b …(ii)
Also, (2, 3) ∈ f
⇒ f(2) = 3
Replacing x by 2 in (i), we have
f(2) = a × 2 + b
⇒ 3 = 2a + b …(iii)
Subtracting (ii) from (iii), we get
2 = a
Putting this value of a in (ii), we get
1 = 2 + b
or
b = −1
Therefore:
a = 2, b = −1
Question 9.
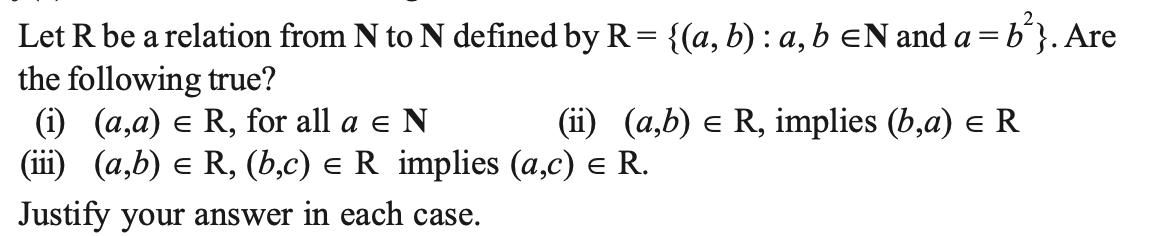
Answer 9.
(i) (a, a) ∈ R for all a ∈ N
For (a, a) to belong to R, we must have
a = a²
This gives
a² − a = 0
a(a − 1) = 0
So, a = 0 or a = 1.
Thus, the condition is not true for all natural numbers.
Conclusion:
Statement (i) is false.
(ii) (a, b) ∈ R ⇒ (b, a) ∈ R
Given (a, b) ∈ R,
a = b²
For (b, a) ∈ R, we must have
b = a²
Substituting a = b²,
b = (b²)² = b⁴
This is not true for all b ∈ N.
Example:
(4, 2) ∈ R since 4 = 2²
But (2, 4) ∉ R since 2 ≠ 4²
Conclusion:
Statement (ii) is false.
(iii) (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R
Given:
(a, b) ∈ R ⇒ a = b²
(b, c) ∈ R ⇒ b = c²
Substituting b = c² in a = b²,
a = (c²)² = c⁴
For (a, c) ∈ R, we need
a = c²
But c⁴ ≠ c² in general.
Example:
(16, 4) ∈ R and (4, 2) ∈ R
But (16, 2) ∉ R
Conclusion:
Statement (iii) is false.
Question 10. Let A ={1,2,3,4}, B = {1,5,9,11,15,16} and f = {(1,5), (2,9), (3,1), (4,5), (2,11)}. Are the following true? (i) f is a relation from A to B (ii) f is a function from A to B. Justify your answer in each case.
Answer 10.
(i)
Every element of f is an element of A × B.
⇒ f ⊂ A × B
⇒ f is a relation from A to B
(since every subset of A × B is a relation from A to B).
(ii)
(2, 9) and (2, 11) both belong to f.
Here, both these points of f have the same first entry.
⇒ f-image of 2 is not unique.
⇒ f is not a function from A to B.
Question 11. Let f be the subset of Z × Z defined by f = {(ab, a + b) : a, b ∈ Z}. Is f a function from Z to Z? Justify your answer.
Answer 11.
Given:
f = { (ab, a + b) : a, b ∈ Z }
Taking a = b = 1, we get
(ab, a + b) = (1, 2) ∈ f
Taking a = b = −1, we get
(ab, a + b) = (1, −2) ∈ f
⇒ f-image of 1 is not unique
⇒ f is not a function.
Question 12. Let A = {9,10,11,12,13} and let f : A→N be defined by f(n) = the highest prime factor of n. Find the range of f.
Answer 12.
Here,
A = {9, 10, 11, 12, 13}
and f(n) = the highest prime factor of n.
The only prime factor of 9 is 3.
⇒ f(9) = 3
Prime factors of 10 are 2 and 5.
⇒ f(10) = 5
The only prime factor of 11 is 11.
⇒ f(11) = 11
Prime factors of 12 are 2 and 3.
⇒ f(12) = 3
The only prime factor of 13 is 13.
⇒ f(13) = 13
Therefore, the range of f is the set of f-images of elements of A.
Range of f
= { f(9), f(10), f(11), f(12), f(13) }
= { 3, 5, 11, 3, 13 }
= { 3, 5, 11, 13 } (dropping repetitions)
