Last Updated:
Written by:
Time to read:
Table of Contents – Class 11 Maths Chapter 2 Exercise 2.3 Solutions
Solved Examples before Exercise 2.3
Example 10. Let N be the set of natural numbers and the relation R be defined on N such that R = {(x, y) : y = 2x, x, y ∈ N}. What is the domain, codomain and range of R? Is this relation a function?
Answer 10.
The domain of R is the set of natural numbers N. The codomain is also N.
The range is the set of even natural numbers.
Since every natural number n has one and only one image, this relation is a function.
Example 12. Let N be the set of natural numbers. Define a real valued function f : N → N by f (x) = 2x + 1. Using this definition, complete the table given below.
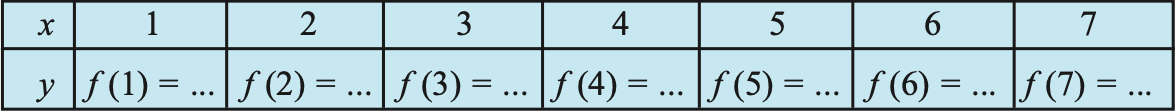
Answer 12.
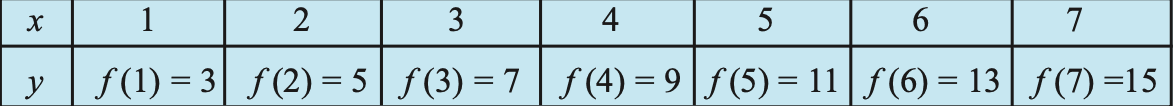
Example 13. Define the function f: R → R by y = f(x) = x2, x ∈ R. Complete the table given below by using this definition. What is the domain and range of this function? Draw the graph of f.

Answer 13.
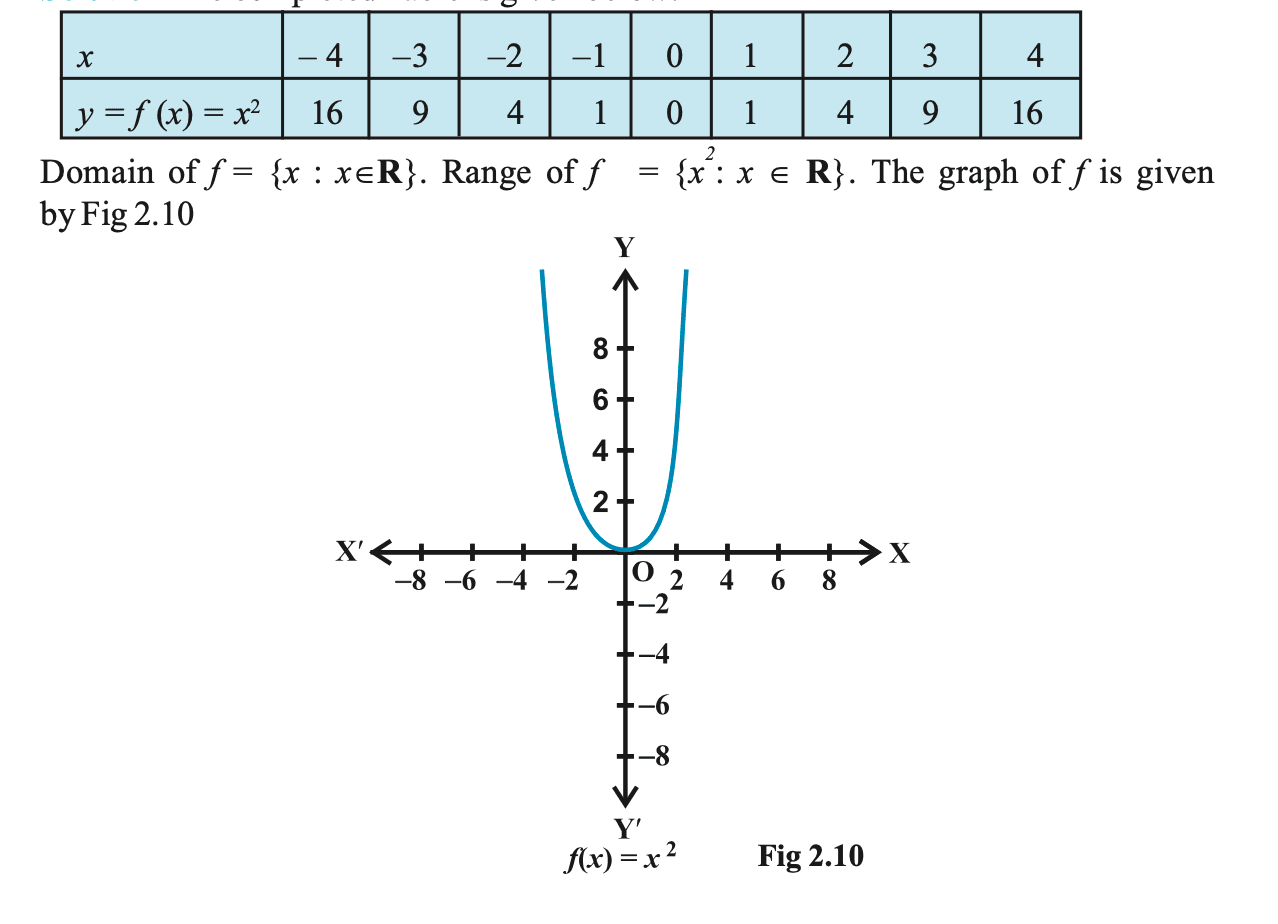
Example 14. Draw the graph of the function f :R → R defined by f (x) = x3, x∈R.
Answer 14.
We have f(0) = 0, f(1) = 1, f(–1) = –1, f(2) = 8, f(–2) = –8, f(3) = 27; f(–3) = –27, etc.
Therefore, f = {(x,x3): x∈R}.
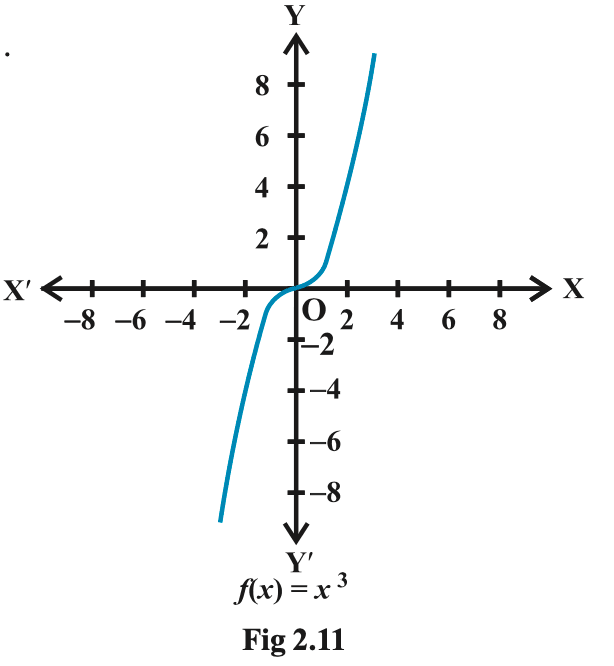
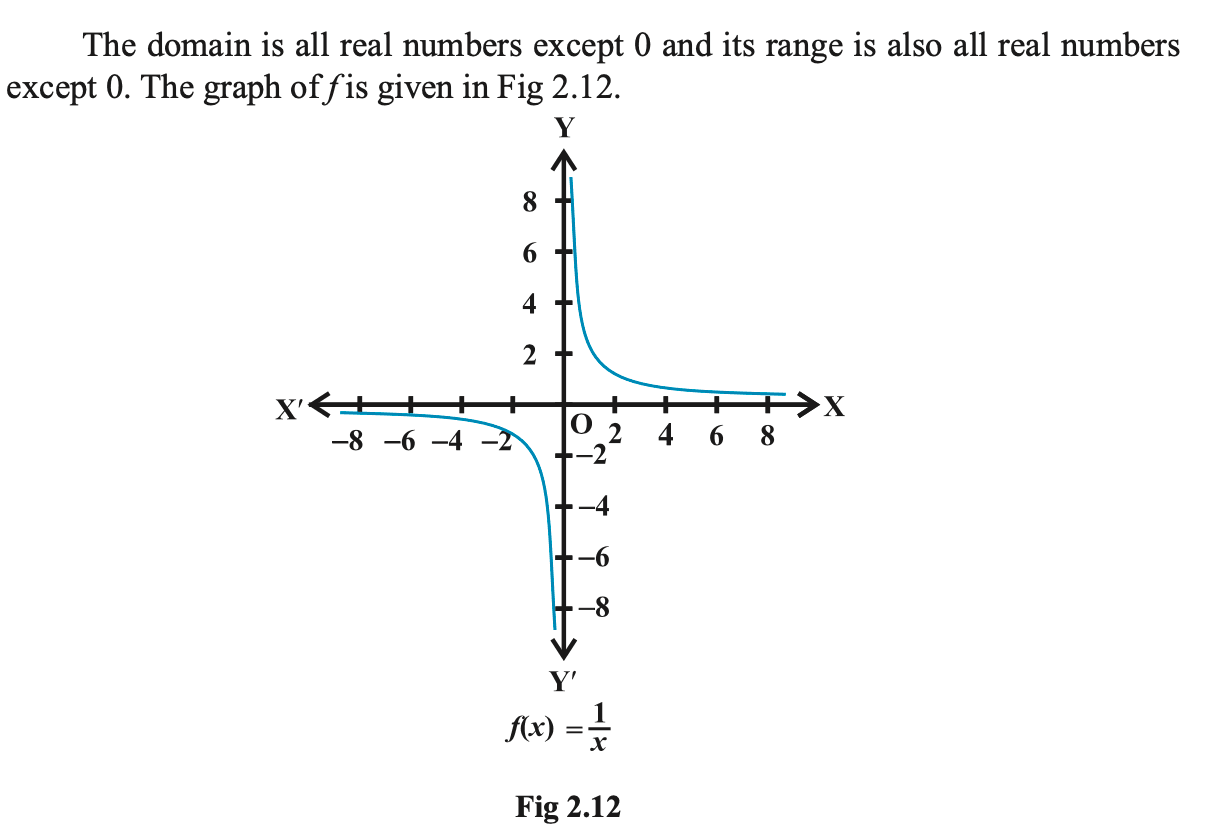
Example 15. Define the real valued function f : R – {0} → R defined by f(x) = 1/x, x ∈ R –{0}. Complete the Table given below using this definition. What is the domain and range of this function?

Answer 15.

Example 16.
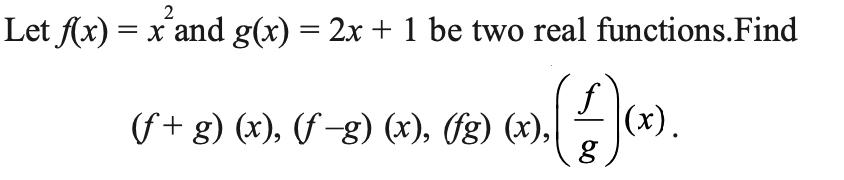
Answer 16.
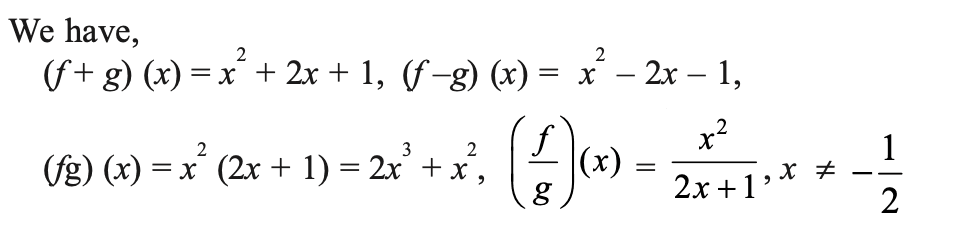
Example 17.
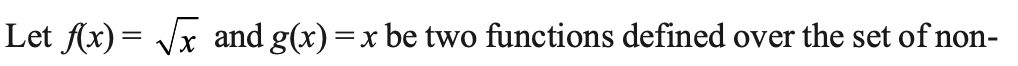
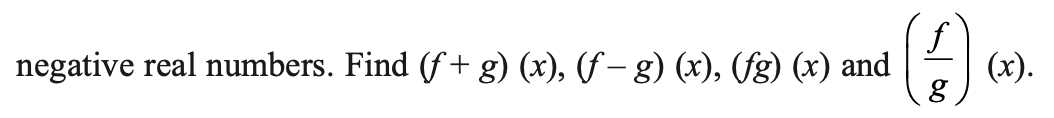
Answer 17.
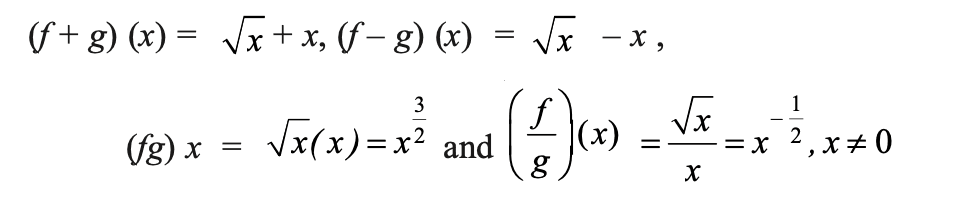
Exercise 2.3 solved questions
Question 1. Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range. (i) {(2,1), (5,1), (8,1), (11,1), (14,1), (17,1)} (ii) {(2,1), (4,2), (6,3), (8,4), (10,5), (12,6), (14,7)} (iii) {(1,3), (1,5), (2,5)}.
Answer 1.
(i) Domain of the relation = {2, 5, 8, 11, 14, 17}
Since every element of the domain has a unique image, this relation is a function.
Domain of the function = {2, 5, 8, 11, 14, 17}
Range of the function = {1}.
(ii) Domain of the relation = {2, 4, 6, 8, 10, 12, 14}
Since every element of the domain has a unique image, this relation is a function.
Domain of the function = {2, 4, 6, 8, 10, 12, 14}
Range of the function = {1, 2, 3, 4, 5, 6, 7}.
(iii) Domain of the relation = {1, 2}
Since the same first element 1 corresponds to two different images 3 and 5, this relation is not a function.
Question 2.

Answer 2. (i) Domain is all real numbers
For all x 𝛜 R, -|x| ≤ 0
So, f(x) ≤ 0
Range of f = (∞,0]
(ii) To find the domain and range of the function
f(x) = √(9 − x²), we follow these steps:
1. Finding the Domain
For a square root function to be defined for real numbers, the expression inside the square root must be greater than or equal to zero.
9 − x² ≥ 0
Solving the inequality:
x² ≤ 9
|x| ≤ √9
−3 ≤ x ≤ 3
Thus, the domain is:
x ∈ [−3, 3]
2. Finding the Range
The range consists of all possible values of f(x) for x in the domain [−3, 3].
Minimum Value
The smallest value of x² is 0 (when x = 0).
However, to minimize the square root, we look for the largest value of x², which is 9 (at x = 3 or x = −3).
f(3) = √(9 − 3²) = √0 = 0
Maximum Value
The square root is maximised when x² is as small as possible.
The smallest value of x² is 0 (at x = 0).
f(0) = √(9 − 0²) = √9 = 3
Since the square root function is continuous and non-negative, the output values vary from 0 to 3.
Thus, the range is:
f(x) ∈ [0, 3]
Question 3. A function f is defined by f(x) = 2x –5. Write down the values of (i) f (0), (ii) f (7), (iii) f (–3).
Answer 3.(i) f(0) = -5
(ii) f(7) = 9
(iii) f(-3) = -11
Question 4.
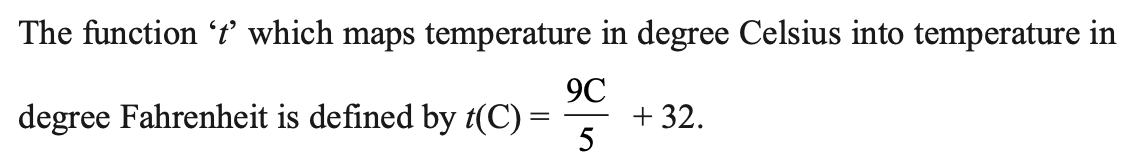
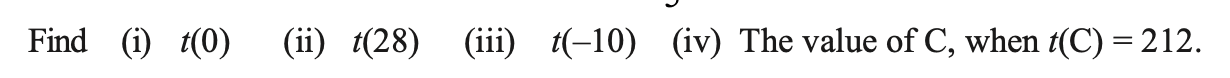
Answer 4.
(i) Replacing C by 0, we have
t(0) = (9 × 0) / 5 + 32
t(0) = 0 + 32
t(0) = 32
(ii) Replacing C by 28, we have
t(28) = (9 × 28) / 5 + 32
t(28) = 252 / 5 + 32
t(28) = 50.4 + 32
t(28) = 82.4
(iii) Replacing C by −10, we have
t(−10) = (9 × (−10)) / 5 + 32
t(−10) = −18 + 32
t(−10) = 14
(iv) Given t(C) = 212
(9C / 5) + 32 = 212
⇒ 9C / 5 = 212 − 32
⇒ 9C / 5 = 180
⇒ C = (5 / 9) × 180
C = 100
Question 5. Find the range of each of the following functions.
(i) f (x) = 2 – 3x, x ∈ R, x > 0.
(ii) f(x) = x2 + 2, x is a real number.
(iii) f (x) = x, x is a real number.
Answer 5.
(i) f(x) = 2 − 3x, x ∈ R, x > 0 (Given)
Consider:
x > 0
Multiplying both sides by −3,
−3x < 0
Adding 2 to both sides,
2 − 3x < 2
Or (by (i)),
f(x) < 2 for x > 0
⇒ f(x) ∈ (−∞, 2)
⇒ Range of this f(x) is (−∞, 2)
Note:
Domain of this f(x) is
{x : x ∈ R, x > 0} = (0, ∞)
(ii)
f(x) = x² + 2, x ∈ R (Given)
x ∈ R ⇒ x² ≥ 0
Adding 2 to both sides,
x² + 2 ≥ 2
Or (by (i)),
f(x) ≥ 2
⇒ f(x) ∈ [2, ∞)
∴ Range of f(x) is [2, ∞)
(iii) f(x) = x, x ∈ R (Given)
⇒ f(x) also takes all real values
∴ Range of f(x) is R
