Last Updated:
Written by : Anmol Gupta
8 mins read time
NCERT Exemplar Class 11 Maths Chapter 1 Sets Exercise Solutions Objective Type Questions
Table of Contents
Solved Objective Type Questions of NCERT Exemplar Sets Exercise
Choose the correct answers from the given four options in each of Questions 29 to 43 (M.C.Q.).
Question 29
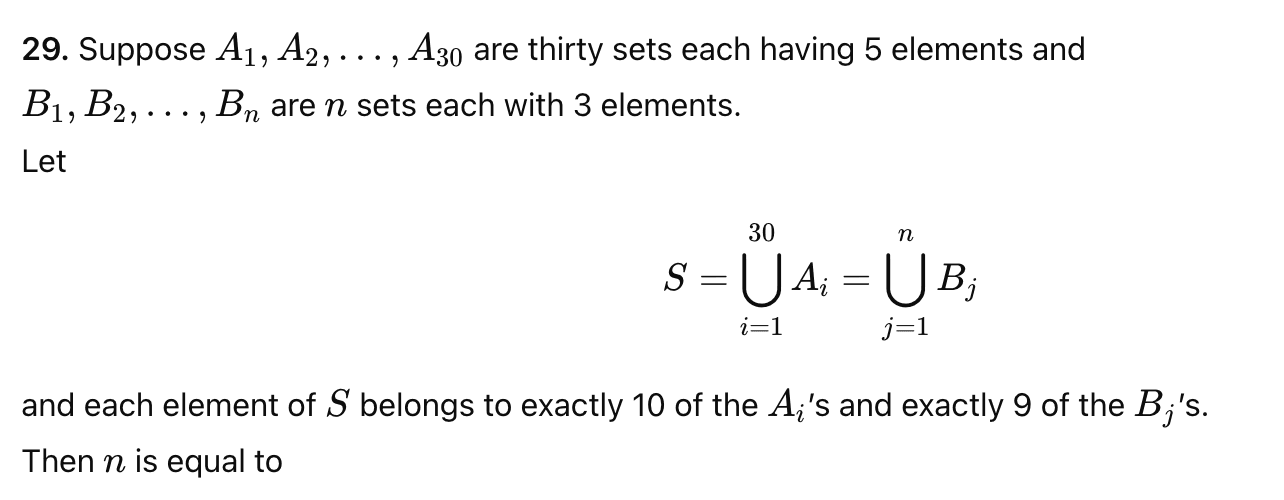
Answer 29
Problem
Suppose A₁, A₂, …, A₃₀ are thirty sets each having 5 elements, and B₁, B₂, …, Bₙ are n sets each having 3 elements.
Let S = A₁ ∪ A₂ ∪ … ∪ A₃₀ = B₁ ∪ B₂ ∪ … ∪ Bₙ.
Each element of S belongs to exactly 10 of the A’s and exactly 9 of the B’s.
Find the value of n.
Step 1 – Counting with A’s
Each Aᵢ has 5 elements, and there are 30 such sets.
Total element–set pairs = 30 × 5 = 150.
But each element of S occurs in 10 of the A’s.
Let the number of distinct elements in S be m.
Then, m × 10 = 150
⟹ m = 15
Hence, S has 15 distinct elements.
Step 2 – Counting with B’s
Each Bⱼ has 3 elements, and there are n such sets.
Total element–set pairs = n × 3.
Each of the 15 elements of S occurs in 9 of the B’s.
Total pairs = 15 × 9 = 135.
Equating both sides:
n × 3 = 135
⟹ n = 45
Final Answer
n = 45
Concept Summary
This problem uses the principle of double counting.
When each element belongs to a fixed number of sets:
(Number of sets) × (Elements per set) = (Number of elements) × (Sets per element)
Applying this rule:
For A’s → 30 × 5 = m × 10 ⇒ m = 15
For B’s → n × 3 = 15 × 9 ⇒ n = 45
Therefore, n = 45.
Question 30 Two finite sets have m and n elements. The number of subsets of the first set is 112 more than that of the second set. The values of m and n are, respectively,
(A) 4, 7 (B) 7, 4 (C) 4, 4 (D) 7, 7
Answer 30.
Number of subsets of a set having m elements = 2ᵐ
and the number of subsets of a set containing n elements = 2ⁿ
As per the given condition,
2ᵐ – 2ⁿ = 112
⇒ 2ⁿ (2ᵐ⁻ⁿ – 1) = 112
⇒ 2ⁿ (2ᵐ⁻ⁿ – 1) = 2⁴ × 7
∴ 2ⁿ = 2⁴ and 2ᵐ⁻ⁿ – 1 = 7
⇒ n = 4 and 2ᵐ⁻ⁿ = 1 + 7 = 8 = 2³
⇒ n = 4 and m – n = 3
⇒ m – 4 = 3 ⇒ m = 7
Hence, the correct option is (b).
Question 31. The set (A ∩ B′)′ ∪ (B ∩ C) is equal to
(A) A′ ∪ B ∪ C (B) A′ ∪ B (C) A′ ∪ C′ (D) A′ ∩ B
Answer 31.
Step 1: Apply De Morgan’s law
(A ∩ B′)′ = A′ ∪ (B′)′
Since (B′)′ = B,
(A ∩ B′)′ = A′ ∪ B
Step 2: Substitute back into the given expression
(A ∩ B′)′ ∪ (B ∩ C) = (A′ ∪ B) ∪ (B ∩ C)
Step 3: Simplify the union
Because (B ∩ C) ⊂ B,
(A′ ∪ B) ∪ (B ∩ C) = A′ ∪ B
Final Answer:
A′ ∪ B
Correct Option: (B)
Question 32. Let F₁ be the set of parallelograms, F₂ the set of rectangles, F₃ the set of rhombuses, F₄ the set of squares and F₅ the set of trapeziums in a plane. Then F₁ may be equal to:
(A) F₂ ∩ F₃ (B) F₃ ∩ F₄ (C) F₂ ∪ F₅ (D) F₂ ∪ F₃ ∪ F₄ ∪ F₁
Answer 32.
We know that rectangles, rhombuses, and squares in a plane are all parallelograms, but a trapezium is not a parallelogram.
Therefore, the set of all parallelograms can be expressed as the union of the sets of rectangles, rhombuses, and squares.
F₁ = F₂ ∪ F₃ ∪ F₄ ∪ F₁
Hence, the correct option is (d).
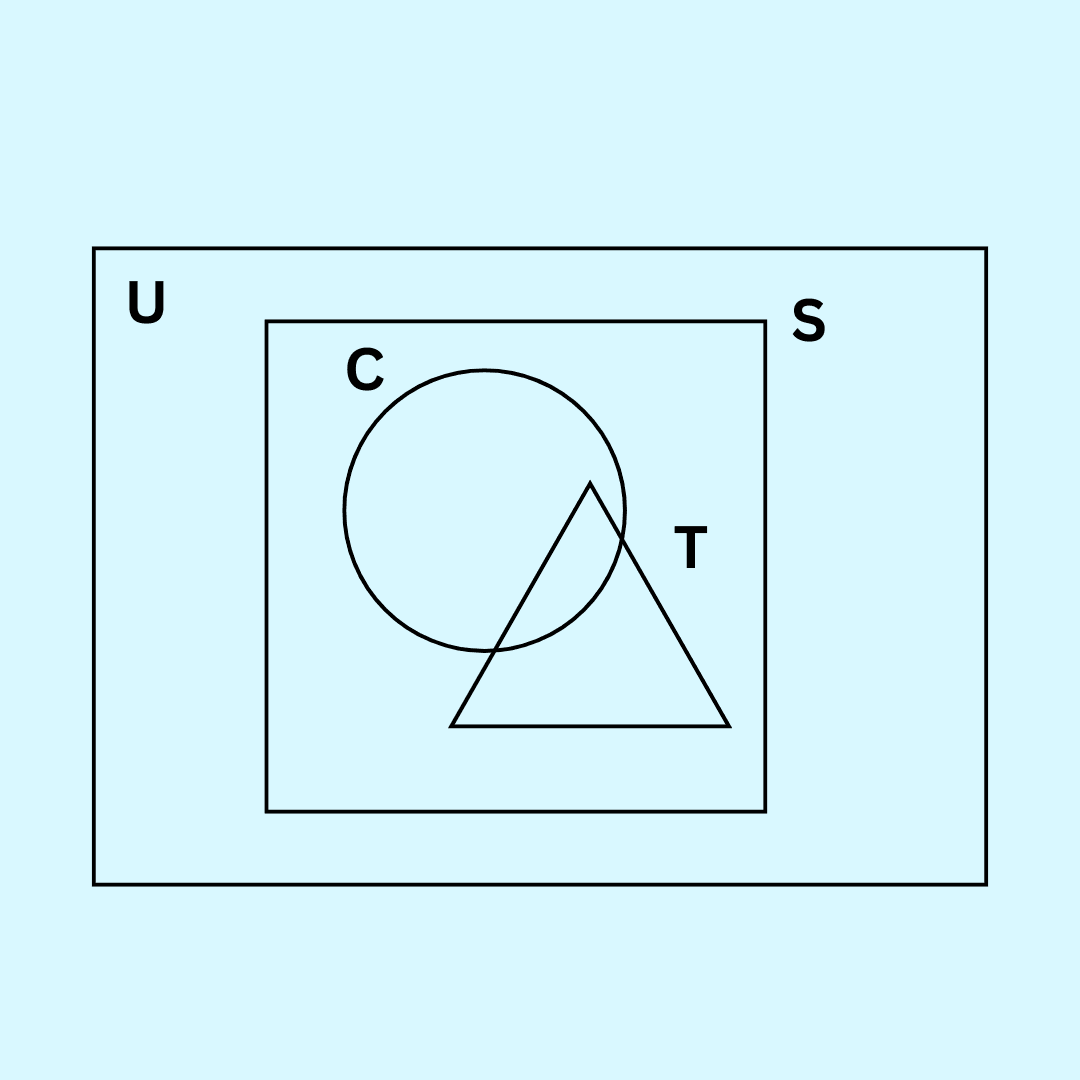
Question 33. Let S = set of points inside the square, T = the set of points inside the triangle and C = the set of points inside the circle. If the triangle and circle intersect each other and are contained in a square. Then
(A) S ∩ T ∩ C = φ (B) S ∪ T ∪ C = C
(C) S ∪ T ∪ C = S (D) S ∪ T = S ∩ C
Answer 33.
The given condition can be shown using a Venn diagram.
From the diagram, it is clear that all the points of triangle and circle lie inside the square.
Therefore,
S ∪ T ∪ C = S
Option (C) is correct
Question 34.
Let R be set of points inside a rectangle of sides a and b (a, b > 1) with two sides along the positive direction of x-axis and y-axis. Then
(A) R = {(x, y) : 0 ≤ x ≤ a, 0 ≤ y ≤ b}
(B) R = {(x, y) : 0 ≤ x < a, 0 ≤ y ≤ b}
(C) R = {(x, y) : 0 ≤ x ≤ a, 0 < y < b}
(D) R = {(x, y) : 0 < x < a, 0 < y < b}
Answer 34
Let OABC be a rectangle whose sides a and b are along the positive direction of the X and Y axes respectively.
Therefore,
R = { (x, y) : 0 < x < a and 0 < y < b }
Hence, the correct option is (D).
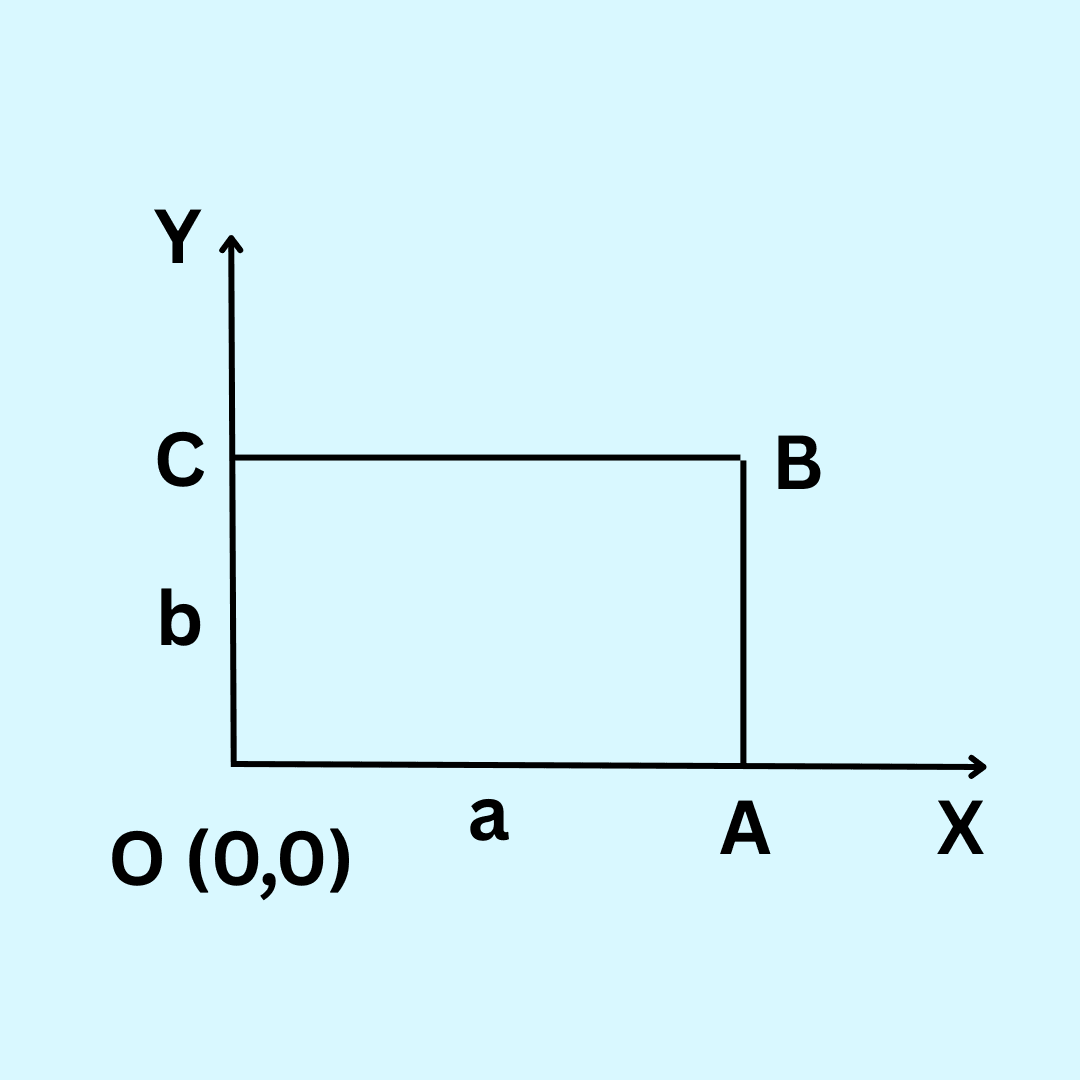
Question 35.
In a class of 60 students, 25 students play cricket and 20 students play tennis, and 10 students play both the games. Then, the number of students who play neither is
(A) 0 (B) 25 (C) 35 (D) 45
Answer 35
Let total number of students = n(U) = 60
Number of students who play Cricket = n(C) = 25
Number of students who play Tennis = n(T) = 20
Number of students who play both Cricket and Tennis = n(C ∩ T) = 10
n(C ∪ T) = n(C) + n(T) – n(C ∩ T)
= 25 + 20 – 10 = 35
Number of students who play neither = n(U) – n(C ∪ T)
= 60 – 35 = 25
Hence, the correct option is (B) 25.
Question 36. In a town of 840 persons, 450 persons read Hindi, 300 read English and 200 read both. Then the number of persons who read neither is
(A) 210 (B) 290 (C) 180 (D) 260
Answer 36
Let total number of persons = n(U) = 840
Number of persons who read Hindi = n(H) = 450
Number of persons who read English = n(E) = 300
Number of persons who read both Hindi and English = n(H ∩ E) = 200
n(H ∪ E) = n(H) + n(E) – n(H ∩ E)
= 450 + 300 – 200
= 550
Number of persons who read neither = n(U) – n(H ∪ E)
= 840 – 550
= 290
Hence, the correct option is (B) 290.
Question 37. If X = { 8ⁿ – 7ⁿ – 1 | n ∈ ℕ } and Y = { 49ⁿ – 49 | n ∈ ℕ }. Then
(A) X ⊂ Y (B) Y ⊂ X (C) X = Y (D) X ∩ Y = φ
Answer 37
Given that
X = { 8n² – 7n – 11 | n ∈ N } = { 0, 49, 490, … }
and
Y = { 49n – 49 | n ∈ N } = { 0, 49, 98, … }
It is clear that every element of X is also present in Y.
∴ X ⊂ Y
Hence, the correct option is (A).
Question 38. A survey shows that 63% of the people watch a News Channel whereas 76% watch another channel. If x% of the people watch both channel, then
(A) x = 35 (B) x = 63 (C) 39 ≤ x ≤ 63 (D) x = 39
Answer 38
Let p% = people watching first news channel = 63%
q% = people watching second channel = 76%
and x% = people watching both channels.
Total ≤ 100% ⇒ p + q – x ≤ 100
⇒ 63 + 76 – x ≤ 100
⇒ x ≥ 39
Also, x ≤ 63 (since it cannot exceed the smaller percentage).
∴ 39 ≤ x ≤ 63
Hence, the correct option is (C).
Question 39.
If sets A and B are defined as
A = { (x, y) | y = 1/x, 0 ≠ x ∈ ℝ }
B = { (x, y) | y = –x, x ∈ ℝ }
then
(A) A ∩ B = A (B) A ∩ B = B (C) A ∩ B = φ (D) A ∪ B = A
Answer 39
We have y = 1/x and y = –x.
For a common element, 1/x = –x ⇒ x² = –1, which has no real solution.
Therefore, A ∩ B = ϕ.
Hence, the correct option is (C).
Question 40. If A and B are two sets, then A ∩ (A ∪ B) equals
(A) A (B) B (C) φ (D) A ∩ B
Answer 40
We know that
A ∩ (A ∪ B) = { x : x ∈ A and x ∈ (A ∪ B) }
= { x : x ∈ A and (x ∈ A or x ∈ B) }
Explanation (Venn Diagram Understanding):
Imagine two circles A and B overlapping in a Venn diagram.
- The union A ∪ B covers both circles together.
- The intersection A ∩ (A ∪ B) means: “Take only the part that is inside A, from the combined region of A and B.”
That’s just A itself.
Therefore, A ∩ (A ∪ B) = A.
= { x : x ∈ A }
= A
Hence, the correct option is (A).
Question 41. If A = {1, 3, 5, 7, 9, 11, 13, 15, 17} B = {2, 4, … , 18} and N the set of natural numbers is the universal set, then A′ ∪ (A ∪ B) ∩ B′) is
(A) φ (B) N (C) A (D) B
Answer 41
Using De Morgan’s law,
(A ∪ B)′ = A′ ∩ B′
⇒ A′ ∪ ((A ∪ B)′ ∩ B′)
= A′ ∪ ((A′ ∩ B′) ∩ B′)
= A′ ∪ (A′ ∩ B′)
= A′ (by absorption law)
Since A′ represents the complement of A with respect to N, we get A′ = N.
Hence, the correct option is (B) N.
Question 42. Let S = {x | x is a positive multiple of 3 less than 100}
P = {x | x is a prime number less than 20}. Then n(S) + n(P) is
(A) 34 (B) 41 (C) 33 (D) 30
Answer 42
S = {3, 6, 9, 12, 15, 18, …, 99}
⇒ n(S) = 33
T = {2, 3, 5, 7, 11, 13, 17, 19}
⇒ n(T) = 8
n(S) + n(T) = 33 + 8 = 41
Hence, the correct option is (B) 41.
Question 43. If X and Y are two sets and X′ denotes the complement of X, then X ∩ (X ∪ Y)′ is equal to (A) X (B) Y (C) φ (D) X ∩ Y
Answer 43
Let x ∈ X ∩ (X ∪ Y)′
⇒ x ∈ X and x ∈ (X ∪ Y)′
⇒ x ∈ X and x ∉ (X ∪ Y)
⇒ x ∈ X and x ∉ X and x ∉ Y
This is impossible as x cannot be both in X and not in X at the same time. Therefore, X ∩ (X ∪ Y)′ = ϕ.
Hence, the correct option is (C) ϕ.

