Last Updated:
Written by:
Time to read:
NCERT Exemplar Class 11 Maths Chapter 1 Sets Exercise Solutions Short Answer Type
Table of Contents
Solved Short Answer Type Questions of NCERT Exemplar Sets Exercise
Question 1 Write the following sets in the roster form
(i) A = {x : x ∈ R, 2x + 11 = 15}
(ii) B = {x | x2 = x, x ∈ R}
(iii) C = {x | x is a positive factor of a prime number p}
Answer 1 (i) 2x + 11 = 15
2x = 4
x =2
A = {2}
(ii) x2 = x
x2 – x = 0
x(x-1) = 0
x=0 or x=1
A set of solutions includes all values that satisfy the equation
Therefore, B = {0,1}
(iii) Positive factors of prime number p are 1 and p
Therefore, C = {1, p}
Question 2 Write the following sets in the roster form
(i) D = {t | t3 = t, t ∈ R}
(ii)
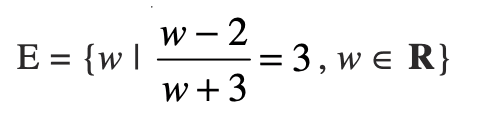
(iii) F = {x | x4 – 5x2 + 6 = 0, x ∈ R}
Answer 2.(i) t3 = t
t3 – t = 0
t3 – t = 0
t(t2-1) = 0
t(t-1)(t+1) = 0
t = 0 or t = 1 or t= -1
D = {0,1,-1}
(ii)
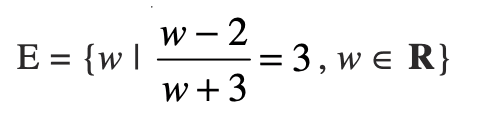
w-2 = 3(w+3)
w-2 = 3w+9
2w = -11
w = ⁻¹¹⁄₂
E = {⁻¹¹⁄₂}
(iii) x4 – 5x2 + 6 = 0
x4 – 3x2 – 2x2 + 6 = 0
x2(x2-3) – 2(x2-3) = 0
(x2 – 2)(x2-3) = 0
(x2 – 2) = 0 or (x2 – 3) = 0
x2 = 2 or x2 = 3
A set of solutions includes all values that satisfy the equation
F =

Question 3. If Y = {x | x is a positive factor of the number 2p – 1 (2p – 1), where 2p – 1 is a prime number}. Write Y in the roster form
Answer 3. Let N = 2p – 1 (2p – 1)
This is the formula for an even perfect number when 2p−1 is a prime number (called a Mersenne prime).
Now:
- 2p – 1 and 2p – 1 are co-prime
- So the total number N is the product of two co-prime numbers
- To get all positive factors of N, we can multiply the factors of each part

Factors of 2p-1 :
These are all powers of 2 up to 2p-1
{1, 2, 22 , 23,…,2p-1}
Explanation of above using example, suppose p=5, then 2p-1= 25-1 = 24 = 16
Factors of 16 = {1, 2, 4, 8, 16} = { 20, 21, 22, 23 , 24 }
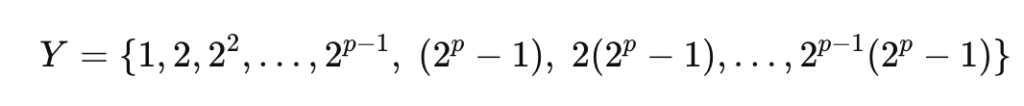
Question 4. State which of the following statements are true and which are false. Justify your answer.
(i) 35 ∈ {x | x has exactly four positive factors}.
(ii) 128 ∈ {y | the sum of all the positive factors of y is 2y}
(iii) 3 ∉ {x | x4 – 5x3 + 2x2 – 112x + 6 = 0}
(iv) 496 ∉ {y | the sum of all the positive factors of y is 2y}.
Answer 4.(i) True as factors of 35 are 1, 5, 7, 35 which are four positive factors
(ii) False
Factors of 128 are 1, 2, 4, 8, 16, 32, 64, 128
Their sum is 1+2+4+8+16+32+64+128 = 255
Which is not equal to 2 × 128
(iii) True
Putting x = 3
34 – 5(3)3 + 2(3)2– 112(3) + 6
= 81 – 135 + 18 – 336 + 6 = -366 ≠ 0
(iv) False
Factors of 496 are 1, 2, 4, 8, 16, 31, 62, 124, 248, 496
Their sum is 1+2+4+8+16+31+62+124+248+496 = 992
496 × 2 = 992
Question 5. Given L = {1, 2, 3, 4}, M = {3, 4, 5, 6} and N = {1, 3, 5}
Verify that L – (M ∪ N) = (L – M) ∩ (L – N)
Answer 5. M ∪ N = {1,3,4,5,6}
L – (M ∪ N) = {2}
L-M = {1,2}
L-N = {2,4}
(L – M) ∩ (L – N) = {2}
Hence, verified
Question 6. If A and B are subsets of the universal set U, then show that
(i) A ⊂ A ∪ B
(ii) A ⊂ B ⇔ A ∪ B = B
(iii) (A ∩ B) ⊂ A
Answer 6. (i) We need to prove that every element of A is also an element of A ∪ B
Let x ∈ A
Then, by the definition of union, since x ∈ A we have: x ∈ A ∪ B
x ∈ A ⇒ x ∈ A ∪ B
Hence A ⊂ A ∪ B
(ii) ⇔ symbol means if and only if
If A ⊂ B
Then let x ∈ A ∪ B
⇒ x ∈ A or x ∈ B
⇒ A ∪ B ⊂ B …(1)
But B ⊂ A ∪ B …(2)
From equations (1) and (2), we get:
A ∪ B = B
Let y ∈ A
⇒ y ∈ (A ∪ B) ⇒ y ∈ B
⇒ y ∈ B ⇔ A ∪ B = B
(iii) Let x ∈ A ∩ B
⇒ x ∈ A and x ∈ B ⇒ x ∈ A
So A ∩ B ⊂ A
Question 7. Given that N = {1, 2, 3, … , 100}. Then write
(i) the subset of N whose elements are even numbers.
(ii) the subset of N whose element are perfect square numbers.
Answer 7. (i) The subset of N whose elements are even numbers is {2, 4, 6, 8, … , 98, 100}
(ii) A perfect square is a number that results from squaring an integer (multiplying an integer by itself)
The subset of N whose element are perfect square numbers is {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}
Question 8. If X = {1, 2, 3}, if n represents any member of X, write the following sets
containing all numbers represented by
(i) 4n (ii) n + 6 (iii) n/2 (iv) n – 1
Answer 8. (i) {4,8,12}
(ii) {7,8,9}
(iii) {½, 1, ³⁄₂}
Question 9. If Y = {1, 2, 3, … 10}, and a represents any element of Y, write the following
sets, containing all the elements satisfying the given conditions.
(i) a ∈ Y but a2 ∉ Y
(ii) a + 1 = 6, a ∈ Y
(iii) a is less than 6 and a ∈ Y
Answer 9. (i) 1 ∈ Y but 12∉ Y, but 12 does belong to Y, so 1 will not be member of below set
2 ∈ Y but 22∉ Y, but 22 does belong to Y, so 2 will not be member of below set
3 ∈ Y but 32∉ Y, but 32 does belong to Y, so 3 will not be member of below set
4 ∈ Y but 42∉ Y, this is true, so 4 will belong to below set. Similarly 5, 6, 7, 8, 9, 10 will belong to below set
{4,5,6,7,8,9,10}
(ii) {5}
(iii) {1,2,3,4,5}
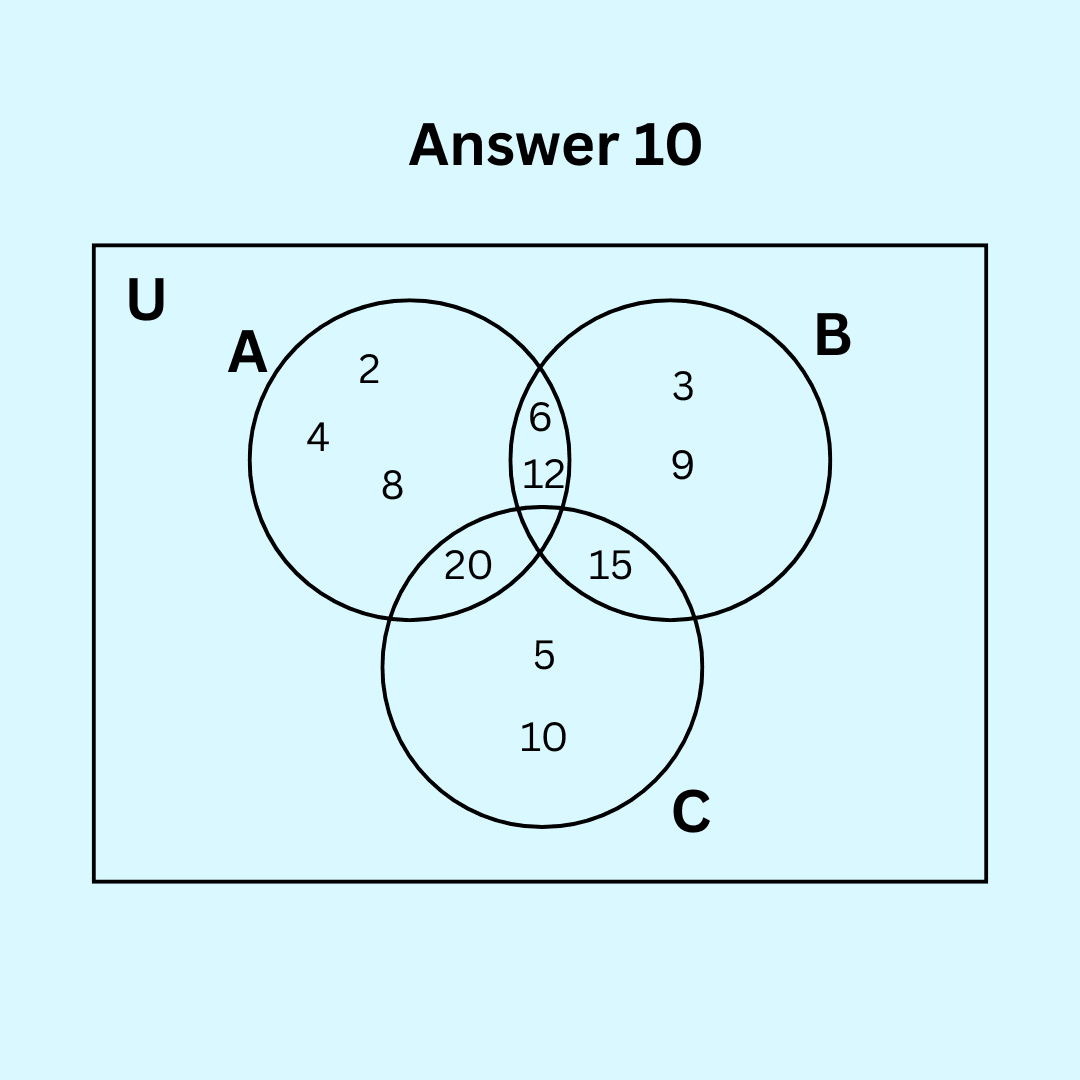
Question 10. A, B and C are subsets of Universal Set U. If A = {2, 4, 6, 8, 12, 20}, B = {3, 6, 9, 12, 15}, C = {5, 10, 15, 20} and U is the set of all whole numbers, draw a Venn diagram showing the relation of U, A, B and C.
Answer 10.
Question 11. Let U be the set of all boys and girls in a school, G be the set of all girls in the school, B be the set of all boys in the school, and S be the set of all students in the school who take swimming. Some, but not all, students in the school take
swimming. Draw a Venn diagram showing one of the possible interrelationship among sets U, G, B and S.
Answer 11.
Question 12. For all sets A, B and C, show that (A – B) ∩ (C – B) = A – (B ∪ C). Determine whether each of the statement in Exercises 13 – 17 is true or false.
Justify your answer.
Answer 12. To prove:
(A – B) ∩ (A – C) = A – (B ∪ C)
Let x ∈ (A – B) ∩ (A – C)
⇒ x ∈ (A – B) and x ∈ (A – C)
⇒ (x ∈ A and x ∉ B) and (x ∈ A and x ∉ C)
⇒ x ∈ A and (x ∉ B and x ∉ C)
⇒ x ∈ A – (B ∪ C)
So, (A – B) ∩ (A – C) ⊂ A – (B ∪ C) …(i)
Let y ∈ A – (B ∪ C)
⇒ y ∈ A and y ∉ (B ∪ C)
⇒ y ∈ A and (y ∉ B and y ∉ C)
⇒ (y ∈ A and y ∉ B) and (y ∈ A and y ∉ C)
⇒ y ∈ (A – B) and y ∈ (A – C)
So, A – (B ∪ C) ⊂ (A – B) ∩ (A – C) …(ii)
From eqn. (i) and (ii), we get:
A – (B ∪ C) = (A – B) ∩ (A – C)
Question 13. For all sets A and B, (A – B) ∪ (A ∩ B) = A
Answer 13. True
(A – B) ∪ (A ∩ B) = [(A – B) ∪ (A)] ∩ [(A – B) U (B)]
= A ∩ ( A U B) = A
Question 14. For all sets A, B and C, A – (B – C) = (A – B) – C
Answer 14. False
Let A = {1,2,3,4,5}
Let B = {5,6,7,8,9}
Let C = {1,9,10,11,12}
B-C = {5,6,7,8}
A – (B – C) = {1,2,3,4} …(1)
A-B = {1,2,3,4}
(A – B) – C = {2,3,4} … (2)
(1) ≠ (2)
Question 15. For all sets A, B and C, if A ⊂ B, then A ∩ C ⊂ B ∩ C
Answer 15. True
Let x ∈ A ∩ C
⇒ x ∈ A and x ∈ C
But A ⊂ B
⇒ x ∈ B and x ∈ C
⇒ x ∈ B ∩ C
⇒ A ∩ C ⊂ B ∩ C
Question 16. For all sets A, B and C, if A ⊂ B, then A ∪ C ⊂ B ∪ C
Answer 16. True
Let x ∈ A ∪ C
⇒ x ∈ A or x ∈ C
⇒ x ∈ B or x ∈ C
⇒ x ∈ B ∪ C
A ∪ C ⊂ B ∪ C
Question 17. For all sets A, B and C, if A ⊂ C and B ⊂ C, then A ∪ B ⊂ C
Answer 17. True
Let x ∈ A ∪ B
⇒ x ∈ A or x ∈ B
⇒ x ∈ C or x ∈ B
⇒ x ∈ C or x ∈ C
⇒ x ∈ C
A ∪ B ⊂ C
Using properties of sets prove the statements given in Exercises 18 to 22
Question 18. For all sets A and B, A ∪ (B – A) = A ∪ B
Answer 18. A ∪ (B – A) = A ∪ ( B ∩ A’ )
= (A ∪ B) ∩ (A ∪ A’) = (A ∪ B) ∩ U
= A ∪ B
Question 19. For all sets A and B, A – (A – B) = A ∩ B
Answer 19. A-B = A ∩ B’
A – (A – B) = A – (A ∩ B’) = A ∩ (A ∩ B’)’ = A ∩ (A’ U (B’)’)
= A ∩ (A’ U B) = (A ∩ A’) U ( A ∩ B ) = ɸ U ( A ∩ B ) = A ∩ B
Question 20. For all sets A and B, A – (A ∩ B) = A – B
Answer 20. L.H.S. = A – (A ∩ B)
= A ∩ (A ∩ B)′
= A ∩ (A′ ∪ B′)
= (A ∩ A′) ∪ (A ∩ B′)
= ɸ ∪ (A – B) [∵ A – B = A ∩ B′]
= A – B = R.H.S.
L.H.S. = R.H.S. Hence proved.
Question 21. For all sets A and B, (A ∪ B) – B = A – B
Answer 21. L.H.S. = (A ∪ B) – B
= (A ∪ B) ∩ B′
= (A ∩ B′) ∪ (B ∩ B′)
= (A – B) ∪ ɸ [∵ A – B = A ∩ B′, and B ∩ B′ = ɸ]
= A – B = R.H.S.
L.H.S. = R.H.S. Hence proved.
Question 22. Let T = { x | ˣ⁺⁵⁄ₓ₋₇ – 5 = ⁴ˣ⁻⁴⁰⁄₁₃₋ₓ }. Is T an empty set? Justify your answer
Answer 22.